Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 588 Дорофеев, Шарыгин — Подробные Ответы
Наблюдаем.
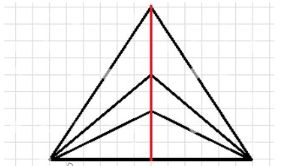
Начертите в тетради несколько равнобедренных треугольников с общим основанием, равным б см. Где расположены вершины этих треугольников?
Вершины таких треугольников расположены на одной прямой, проходящей через середину основания треугольников, другими словами, на оси симметрии треугольников.
Наблюдая за этим, мы видим, что все вершины равнобедренных треугольников находятся на одной прямой, которая делит основание пополам. Эта линия также является осью симметрии для каждого из треугольников. С каждым новым треугольником, добавляемым к ряду, вершины будут всегда располагаться вдоль этой оси симметрии, сохраняя симметричное расположение относительно основания.
Итак, вершины треугольников находятся на оси симметрии, проходящей через середину их основания, что подтверждается графическим изображением на картинке.
Вершины таких треугольников расположены на одной прямой, проходящей через середину основания треугольников, другими словами, на оси симметрии треугольников. Это очень важное наблюдение, так как оно описывает свойства всех равнобедренных треугольников, независимо от их размера или формы, при условии, что они имеют одинаковое основание.
Когда мы рисуем несколько равнобедренных треугольников с общим основанием, то обязательно должны помнить, что все вершины этих треугольников будут располагаться вдоль одной и той же вертикальной прямой. Эта прямая будет проходить через середину основания треугольников. Важно заметить, что такая прямая называется осью симметрии, так как она делит каждый треугольник пополам и делает две его части зеркально симметричными относительно этой оси.
Каждый новый равнобедренный треугольник будет добавляться к существующему ряду таким образом, что его вершина всегда будет на этой оси симметрии. Это означает, что все треугольники будут одинаково ориентированы по отношению к основанию, и их симметричность будет сохраняться. Эта ось симметрии, как и основание, остается неизменной для всех треугольников в ряду.
В результате мы получаем красивую и симметричную картину, где вершины треугольников ровно выстроены на одной прямой, а все треугольники имеют одинаковую ориентацию и симметрию. Это также помогает нам лучше понять и визуализировать структуру равнобедренных треугольников и их взаимосвязь.
