Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 584 Дорофеев, Шарыгин — Подробные Ответы
Ищем закономерность.
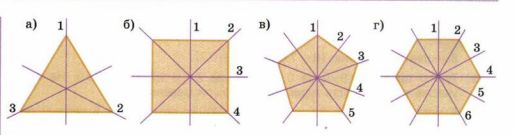
Сколько осей симметрии у правильного треугольника? четырёхугольника? пятиугольника? шестиугольника (см. рис. 7.15)? Сколько осей симметрии у правильного девятиугольника? десятиугольника? Нарисуйте эти фигуры от руки и проведите их оси симметрии. Сколько осей симметрии у правильного n-угольника?
Правильные многоугольники и их оси симметрии:
- Правильный треугольник — 3 оси симметрии.
- Правильный четырёхугольник (квадрат) — 4 оси симметрии.
- Правильный пятиугольник — 5 осей симметрии.
- Правильный шестиугольник — 6 осей симметрии.
- Правильный девятиугольник — 9 осей симметрии.
- Правильный десятиугольник — 10 осей симметрии.
- Правильный n-угольник — n осей симметрии.
Правильные многоугольники и их оси симметрии:
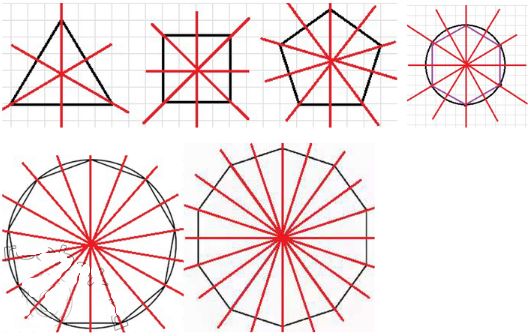
Правильные многоугольники обладают осевыми симметриями, которые делят фигуру на одинаковые зеркальные части. Количество осей симметрии для каждого многоугольника зависит от количества его сторон. Рассмотрим различные правильные многоугольники и количество осей симметрии для каждого из них:
- Правильный треугольник — 3 оси симметрии. Это означает, что правильный треугольник можно разделить на три одинаковые части с помощью осей симметрии, которые проходят через его вершины и середины противоположных сторон. Эти оси пересекаются в центре треугольника.
- Правильный четырёхугольник (квадрат) — 4 оси симметрии. У квадрата есть две оси симметрии, проходящие через середины противоположных сторон, и две диагонали, которые также являются осями симметрии. Все эти оси делят квадрат на две одинаковые части, обеспечивая его симметричность.
- Правильный пятиугольник — 5 осей симметрии. В правильном пятиугольнике можно провести 5 осей симметрии, каждая из которых проходит через одну из вершин и середину противоположной стороны. Эти оси разделяют фигуру на пять равных частей, каждая из которых является зеркальным отражением другой.
- Правильный шестиугольник — 6 осей симметрии. Правильный шестиугольник обладает шестью осями симметрии, которые проходят через противоположные вершины и середины сторон. Эти оси обеспечивают симметричность фигуры и делят её на шесть равных частей.
- Правильный девятиугольник — 9 осей симметрии. Девятиугольник имеет девять осей симметрии, которые проходят через его вершины и середины противоположных сторон. Все эти оси делают девятиугольник идеально симметричным, разделяя его на девять равных частей.
- Правильный десятиугольник — 10 осей симметрии. У десятиугольника есть десять осей симметрии, которые проходят через вершины и середины сторон. Это позволяет делить фигуру на десять равных частей, каждая из которых зеркально отражает другую.
- Правильный n-угольник — n осей симметрии. У правильного многоугольника с n сторонами будет столько же осей симметрии, сколько сторон у этого многоугольника. Оси проходят через вершины и середины противоположных сторон.
