Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 579 Дорофеев, Шарыгин — Подробные Ответы
Экспериментируем.
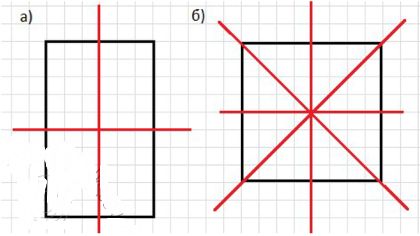
а) Возьмите прямоугольный лист бумаги и найдите оси симметрии этого прямоугольника путём перегибания. Начертите в тетради прямоугольник и проведите его оси симметрии. Является ли диагональ осью симметрии прямоугольника?
б) У квадрата 4 оси симметрии. Найдите их с помощью перегибания. Начертите в тетради квадрат и проведите его оси симметрии.
а) Диагональ не является осью симметрии прямоугольника.
б) У квадрата диагонали являются осями симметрии.
Экспериментируем:
а) Диагональ не является осью симметрии прямоугольника:
- На изображении прямоугольника видно, что при перегибании по диагонали части прямоугольника не совпадают. Это свидетельствует о том, что диагональ не является осью симметрии для прямоугольника.
- Прямоугольник имеет две оси симметрии, которые проходят через середины противоположных сторон, но диагонали не делят прямоугольник на две симметричные части.
б) У квадрата диагонали являются осями симметрии:
- На изображении квадрата видно, что диагонали проходят через противоположные углы и являются осями симметрии. При перегибании квадрата вдоль этих диагоналей части квадрата будут идеально совпадать, что подтверждает их симметричность.
- Таким образом, квадрат обладает четырьмя осями симметрии: две оси проходят через середины сторон, а две другие — через диагонали.
