Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 569 Дорофеев, Шарыгин — Подробные Ответы
Верно или неверно.
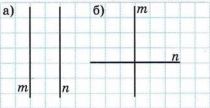
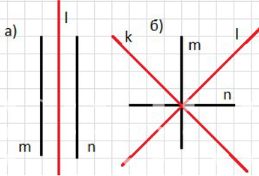
1) Постройте прямую, относительно которой прямая m симметрична прямой n (рис. 7.10). Сколько таких прямых можно построить?
2) Верно ли утверждение: «Для любых двух прямых a и b существует прямая c, относительно которой прямые a и b симметричны»? Обоснуйте свой ответ.
1)
а) Для случая с параллельными прямыми m и n существует только одна прямая, относительно которой они симметричны. Эта прямая проходит ровно посередине между ними и параллельна им.
б) Для случая с пересекающимися прямыми m и n таких прямых две. Это биссектрисы углов, образованных пересечением прямых. Они являются осями симметрии, относительно которых прямые симметричны.
2) Утверждение, что для любых двух прямых a и b существует прямая c, относительно которой они симметричны, верно по следующим причинам:
- Если прямые параллельны, прямая c будет параллельна им и расположена строго посередине между ними.
- Если прямые перпендикулярны, прямая c будет одной из биссектрис углов, образованных при их пересечении.
- Если прямые лежат в разных плоскостях, можно объединить два предыдущих случая и найти прямую c, относительно которой они симметричны.
Таким образом, ось симметрии существует во всех перечисленных случаях.
1) Рассмотрим два случая для прямых m и n:
а) Если прямые m и n параллельны, то существует ровно одна прямая, относительно которой они симметричны. Эта прямая проходит точно посередине между m и n и сама параллельна им. Таким образом, если нарисовать две параллельные прямые, ось симметрии — это линия, расположенная на равном расстоянии от обеих прямых.
б) Если прямые m и n пересекаются, то существует две оси симметрии — это биссектрисы углов, которые образуются в точке их пересечения. Каждая из этих биссектрис является прямой, относительно которой одна прямая является зеркальным отражением другой. Поэтому в данном случае существует две такие прямые.
2) Рассмотрим утверждение: «Для любых двух прямых a и b существует прямая c, относительно которой прямые a и b симметричны». Это утверждение верно по следующим причинам:
- Если прямые a и b параллельны, то прямая c, являющаяся осью симметрии, будет параллельна им и расположена ровно посередине между ними. В этом случае прямая c единственная.
- Если прямые a и b перпендикулярны, то прямая c — это одна из биссектрис углов, образованных пересечением прямых. Таких биссектрис две, и каждая из них служит осью симметрии.
- Если прямые a и b лежат в разных плоскостях, можно рассмотреть их проекции или объединить предыдущие случаи, чтобы найти прямую c, относительно которой они симметричны. В этом случае ось симметрии существует благодаря пространственному расположению прямых.
Таким образом, во всех перечисленных случаях для любых двух прямых можно найти прямую оси симметрии, относительно которой эти прямые являются зеркальными отражениями друг друга.
