ГДЗ по Математике 6 Класс Номер 556 Дорофеев, Шарыгин — Подробные Ответы

Анализируем.
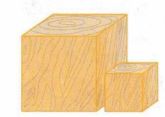
Ребро одного куба равно 10 см, а другого — 5 см (рис. 6.13). Найдите отношение:
1) ребра малого куба к ребру большого куба;
2) площади грани малого куба к площади грани большого куба;
3) объёма малого куба к объёму большого куба.
Есть ли среди этих отношений равные?

1) Отношение ребра малого куба к ребру большого куба:
\( 5 : 10 = \frac{5}{10} = \frac{1}{2} = 0,5 \).

2) Отношение площади грани малого куба к площади грани большого куба:
\( (5 \cdot 5) : (10 \cdot 10) = \frac{25}{100} = \frac{1}{4} = 0,25 \).

3) Отношение объема малого куба к объему большого куба:
\( (5 \cdot 5 \cdot 5) : (10 \cdot 10 \cdot 10) = \frac{125}{1000} = \frac{1}{8} = 0,125 \).

Среди данных отношений нет равных.

1) Отношение ребра малого куба к ребру большого куба определяется как отношение длины ребра меньшего куба к длине ребра большего куба. Если ребро малого куба равно 5, а ребро большого куба равно 10, то это отношение записывается как \( 5 : 10 \). Для удобства вычислений его можно представить в виде дроби \( \frac{5}{10} \), что сокращается до \( \frac{1}{2} \). В десятичном виде это равно 0,5. Таким образом, ребро малого куба в два раза меньше ребра большого куба.

2) Площадь грани куба вычисляется как квадрат длины его ребра, так как грань куба — это квадрат. Для малого куба площадь грани будет равна \( 5^2 = 25 \), а для большого куба — \( 10^2 = 100 \). Отношение площади грани малого куба к площади грани большого куба записывается как \( 25 : 100 \), или \( \frac{25}{100} \). Эта дробь сокращается до \( \frac{1}{4} \), что в десятичном виде равно 0,25. Это означает, что площадь грани малого куба составляет четверть площади грани большого куба.

3) Объем куба рассчитывается как куб длины его ребра, то есть \( a^3 \), где \( a \) — длина ребра. Для малого куба объем равен \( 5^3 = 125 \), а для большого куба — \( 10^3 = 1000 \). Отношение объема малого куба к объему большого куба — это \( 125 : 1000 \), или \( \frac{125}{1000} \). Эта дробь сокращается до \( \frac{1}{8} \), что в десятичном виде равно 0,125. Таким образом, объем малого куба составляет одну восьмую объема большого куба.

Сравнивая полученные отношения, можно заметить, что ни одно из них не равно другому: \( 0,5 \neq 0,25 \neq 0,125 \). Следовательно, среди данных отношений нет равных.