ГДЗ по Математике 6 Класс Номер 54 Дорофеев, Шарыгин — Подробные Ответы

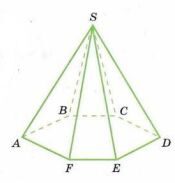
Назовите многогранник, изображённый на рисунке 1.6. Назовите грани, являющиеся видимыми. Перечертите его так, чтобы грань SFE была невидимой.

На рисунке 1.6 изображена пирамида с основанием в виде шестиугольника (шестиугольная пирамида).

1) Многогранник – шестиугольная пирамида \(SABCDEF\), так как основание состоит из шестиугольника \(ABCDEF\), а все боковые грани соединены с вершиной \(S\).

2) Видимые грани: \(SAF\), \(SFE\), \(SED\), так как их стороны на рисунке изображены сплошными линиями, а не пунктиром.

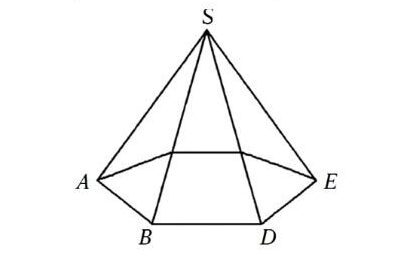
3) Чтобы грань \(SFE\) была невидимой, нужно перерисовать пирамиду, повернув её так, чтобы вершины \(E\) и \(F\) оказались сзади, и тогда грань \(SFE\) проводится пунктиром, а передними видимыми гранями будут, например, \(SAB\), \(SBC\), \(SCD\).

На рисунке 1.6 изображён многогранник, который представляет собой правильную пирамиду с шестигранным основанием. Такая пирамида состоит из основания в виде правильного шестиугольника и вершины, соединённой с каждым из шести углов основания с помощью боковых граней в форме треугольников.

1) Многогранник на рисунке – шестиугольная пирамида \(SABCDEF\). Основание этой пирамиды представляет собой шестиугольник с вершинами \(A,B,C,D,E,F\), лежащими в одной плоскости. Отдельная вершина \(S\) не лежит в плоскости основания и соединена отрезками со всеми вершинами шестиугольника. Именно такая фигура по определению называется пирамидой с шестиугольным основанием: любое сечение через вершину \(S\) и одну сторону основания даёт треугольную боковую грань, поэтому все боковые грани – треугольники вида \(SAB\), \(SBC\), \(SCD\), \(SDE\), \(SEF\), \(SFA\).

2) Чтобы определить видимые грани, рассматриваем, какие рёбра изображены сплошными линиями, а какие пунктиром. Сплошные линии на рисунке показывают элементы, находящиеся ближе к наблюдателю. В основе шестиугольника видимы рёбра \(AB\), \(BC\), \(CD\) и \(DE\), а рёбра, уходящие назад, либо частично закрыты, либо изображены пунктиром. Боковые грани, полностью ограниченные сплошными рёбрами, считаются видимыми. Такими гранями являются треугольники \(SAF\), \(SFE\), \(SED\). Их стороны \(SA\), \(AF\), \(SF\), \(FE\), \(SE\), \(ED\) даны на чертеже сплошными линиями, что означает, что эти грани расположены на передней, обращённой к наблюдателю части поверхности пирамиды и не закрываются другими гранями.

3) Чтобы перерисовать пирамиду так, чтобы грань \(SFE\) стала невидимой, мысленно поворачиваем фигуру вокруг вертикальной оси, проходящей через вершину \(S\) и центр основания. Наша цель – «увести» треугольник \(SFE\) за переднюю часть фигуры, то есть расположить его сзади относительно точки наблюдения. На новом чертеже точки \(E\) и \(F\) нужно изобразить так, чтобы они оказались дальше от наблюдателя, а передними вершинами основания стали, например, \(A\), \(B\), \(C\) и \(D\). Тогда грани, обращённые к нам, будут \(SAB\), \(SBC\), \(SCD\), возможно \(SDA\), и их рёбра надо выполнить сплошными. Грани же, которые окажутся на задней стороне пирамиды, в том числе \(SFE\), следует показать пунктиром: рёбра \(SF\), \(FE\) и \(SE\) изображаются штриховой линией, что и будет обозначать невидимость грани \(SFE\) при новом положении пирамиды относительно наблюдателя.