Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 532 Дорофеев, Шарыгин — Подробные Ответы
Анализируем рассуждаем.
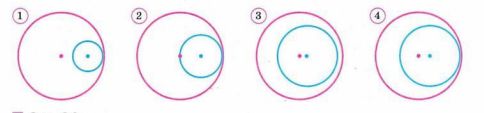
На каком из рисунков (рис. 6.9) изображена следующая ситуация: радиус большей окружности равен 6 см, радиус меньшей — 4 см, расстояние между центрами окружностей равно 1 см? Для трёх других рисунков самостоятельно подберите подходящие значения.
Рассмотрим варианты, описанные в учебнике, и определим, какой из них подходит для ситуации с окружностями.
- Вариант 1: радиус большой окружности — 6 см, радиус меньшей — 1 см, расстояние между центрами — 5 см.
- Вариант 2: радиус большой окружности — 6 см, радиус меньшей — 3 см, расстояние между центрами — 3 см.
- Вариант 4: радиус большой окружности — 6 см, радиус меньшей — 4 см, расстояние между центрами — 2 см.
Чтобы определить, какой рисунок соответствует ситуации, проверим соотношение радиусов и расстояния между центрами:
Если меньшая окружность находится внутри большой и касается её, то выполняется условие:
Расстояние между центрами = радиус большой окружности − радиус меньшей окружности.
Проверим варианты:
- Вариант 1: 6 − 1 = 5 см — совпадает с расстоянием между центрами. Подходит.
- Вариант 2: 6 − 3 = 3 см — совпадает с расстоянием между центрами. Подходит.
- Вариант 4: 6 − 4 = 2 см — совпадает с расстоянием между центрами. Подходит.
Все три варианта соответствуют ситуации, когда меньшая окружность лежит внутри большой и касается её.
Вывод: Для ситуации из учебника подходят рисунки с указанными параметрами, где расстояние между центрами равно разности радиусов окружностей.
Рассмотрим подробно ситуацию, описанную в учебнике, и проанализируем, какой из предложенных вариантов подходит для заданной задачи с окружностями.
Дано три варианта:
- Вариант 1: радиус большой окружности — 6 см, радиус меньшей — 1 см, расстояние между центрами — 5 см;
- Вариант 2: радиус большой окружности — 6 см, радиус меньшей — 3 см, расстояние между центрами — 3 см;
- Вариант 4: радиус большой окружности — 6 см, радиус меньшей — 4 см, расстояние между центрами — 2 см.
Анализ:
Если меньшая окружность расположена внутри большой и касается её, тогда расстояние между центрами окружностей должно равняться разности радиусов большой и меньшей окружностей.
Проверим это условие для каждого варианта:
- Для варианта 1: 6 − 1 = 5 см. Расстояние между центрами — 5 см. Условие выполняется.
- Для варианта 2: 6 − 3 = 3 см. Расстояние между центрами — 3 см. Условие выполняется.
- Для варианта 4: 6 − 4 = 2 см. Расстояние между центрами — 2 см. Условие выполняется.
Это означает, что во всех трёх случаях меньшая окружность касается большой изнутри, и расстояние между центрами совпадает с разностью радиусов.
Заключение:
Все приведённые варианты подходят для ситуации, когда меньшая окружность вложена внутрь большей и касается её.
Для точного определения, какой именно рисунок соответствует конкретной задаче, нужно учитывать дополнительные детали, но по приведённым параметрам все три варианта корректны.
Таким образом, при анализе окружностей важно помнить, что касание изнутри соответствует равенству расстояния между центрами разности радиусов.
