Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 531 Дорофеев, Шарыгин — Подробные Ответы
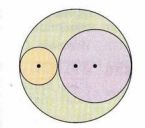
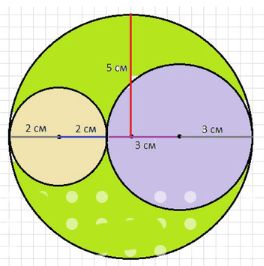
Радиус меньшей окружности равен 2 см, радиус средней — 3 см (рис. 6.8). Чему равен радиус большей окружности? Воспроизведите рисунок.
Рассмотрим решение задачи.
Диаметр меньшей окружности:
2 × 2 = 4 см.
Диаметр средней окружности:
3 × 2 = 6 см.
Диаметр большей окружности равен сумме диаметров меньшей и средней окружностей:
4 + 6 = 10 см.
Радиус большей окружности равен половине диаметра:
10 ÷ 2 = 5 см.
Ответ: радиус большей окружности равен 5 см.
Рассмотрим задачу по вычислению радиуса большей окружности более подробно, используя данные о диаметрах и радиусах меньших окружностей.
Дано:
- Радиус меньшей окружности равен 2 см;
- Радиус средней окружности равен 3 см;
- Требуется найти радиус большей окружности, которая охватывает обе меньшие окружности.
Шаг 1. Найдём диаметр меньшей окружности.
Диаметр равен удвоенному радиусу:
2 × 2 = 4 см.
Шаг 2. Найдём диаметр средней окружности.
Аналогично:
2 × 3 = 6 см.
Шаг 3. Определим диаметр большей окружности.
Большая окружность охватывает обе меньшие, которые касаются друг друга, поэтому диаметр большей окружности равен сумме диаметров меньшей и средней окружностей:
4 + 6 = 10 см.
Шаг 4. Найдём радиус большей окружности.
Радиус — это половина диаметра:
10 ÷ 2 = 5 см.
Итог:
Радиус большей окружности равен 5 см.
Таким образом, используя понятия диаметра и радиуса, а также геометрическое расположение окружностей, мы нашли необходимый радиус.
