Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 506 Дорофеев, Шарыгин — Подробные Ответы
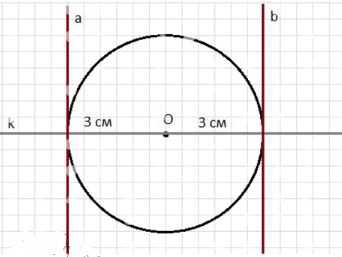
Начертите окружность радиусом 3 см. Через центр окружности проведите прямую k. Постройте касательные к окружности, перпендикулярные прямой k. Чему равно расстояние между этими касательными?
Рассмотрим задачу по шагам:
Дано:
- Окружность с радиусом 3 см;
- Через центр окружности проведена прямая k;
- Необходимо построить касательные к окружности, которые перпендикулярны прямой k;
- Найти расстояние между этими касательными.
Шаг 1: Описание окружности
Окружность радиуса 3 см имеет центр O. Прямая k проходит через центр O, значит она является диаметральной осью окружности.
Шаг 2: Построение касательных, перпендикулярных прямой k
Касательная к окружности — это прямая, которая касается окружности в одной точке и перпендикулярна радиусу, проведённому в точку касания.
Если прямая k проходит через центр, то касательные, перпендикулярные k, будут параллельны друг другу и пересекать окружность в двух точках, находящихся на расстоянии радиуса от центра по направлению, перпендикулярному k.
Шаг 3: Определение расстояния между касательными
Расстояние между двумя параллельными касательными к окружности, перпендикулярными диаметру, равно длине хорды, параллельной диаметру, проходящей через точки касания.
Так как касательные перпендикулярны k, и расстояние от центра до каждой касательной равно радиусу окружности (3 см), расстояние между этими двумя касательными равно:
2 × радиус = 2 × 3 см = 6 см.
Ответ: расстояние между касательными равно 6 см.
Рассмотрим задачу подробно и поэтапно.
Исходные данные:
- Дана окружность с радиусом 3 см и центром O.
- Через центр окружности проведена прямая k.
- Требуется построить касательные к окружности, которые перпендикулярны прямой k.
- Необходимо найти расстояние между этими касательными.
Шаг 1: Анализ расположения прямой k
Прямая k, проходящая через центр окружности, является диаметром этой окружности. Она делит окружность на две половины.
Шаг 2: Свойства касательных, перпендикулярных прямой k
Касательная к окружности в точке касания перпендикулярна радиусу, проведённому в эту точку. Если нам нужно построить касательные, перпендикулярные прямой k, значит, точки касания должны лежать на двух точках окружности, расположенных на прямой, перпендикулярной k и проходящей через центр O.
Иными словами, если прямая k — это ось X, то касательные будут параллельны оси Y и расположены на расстоянии радиуса от центра по обе стороны от прямой k.
Шаг 3: Определение расстояния между касательными
Расстояние между двумя параллельными касательными к окружности, которые перпендикулярны диаметру k, равно удвоенному расстоянию от центра до каждой касательной. Поскольку каждая касательная касается окружности, расстояние от центра O до касательной равно радиусу окружности, то есть 3 см.
Таким образом, расстояние между касательными:
Расстояние = 2 × радиус = 2 × 3 см = 6 см.
Вывод:
Расстояние между двумя касательными, перпендикулярными диаметру окружности с радиусом 3 см, равно 6 сантиметрам.
Эта задача иллюстрирует основные свойства касательных к окружности и взаимное расположение прямых относительно центра окружности.
