
Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 46 Дорофеев, Шарыгин — Подробные Ответы
Найдите значение выражения:
а) \(\frac{1 — \frac{1}{5}}{2} = \frac{\frac{4}{5}}{2} = \frac{4}{5} \cdot \frac{1}{2} = \frac{2}{5}\)
б) \(\frac{6}{1 — \frac{1}{3}} = \frac{6}{\frac{2}{3}} = 6 \cdot \frac{3}{2} = 9\)
в) \(\frac{\frac{2}{3} + \frac{1}{6}}{3} = \frac{\frac{5}{6}}{3} = \frac{5}{6} \cdot \frac{1}{3} = \frac{5}{18}\)
г) \(\frac{1 — \frac{1}{6}}{2 + \frac{1}{6}} = \frac{\frac{5}{6}}{\frac{13}{6}} = \frac{5}{6} \cdot \frac{6}{13} = \frac{5}{13}\)
д) \(\frac{\frac{17}{100} — \frac{1}{10}}{10} = \frac{\frac{7}{100}}{10} = \frac{7}{100} \cdot \frac{1}{10} = \frac{7}{1000}\)
е) \(\frac{\frac{1}{4} + \frac{2}{3}}{2 — \frac{1}{6}} = \frac{\frac{11}{12}}{\frac{11}{6}} = \frac{11}{12} \cdot \frac{6}{11} = \frac{1}{2}\)
а) Рассмотрим выражение \( \frac{1 — \frac{1}{5}}{2} \). Сначала нужно вычислить числитель, то есть \(1 — \frac{1}{5}\). Чтобы вычесть дробь из целого числа, целое число представим как дробь с тем же знаменателем: \(1 = \frac{5}{5}\). Тогда \( \frac{5}{5} — \frac{1}{5} = \frac{4}{5} \). Теперь числитель равен \( \frac{4}{5} \).
Далее делим числитель на 2, что эквивалентно умножению на обратное число: \( \frac{4}{5} \div 2 = \frac{4}{5} \times \frac{1}{2} \). Умножаем числители и знаменатели: \( \frac{4 \times 1}{5 \times 2} = \frac{4}{10} \). Сокращаем дробь, разделив числитель и знаменатель на 2: \( \frac{4}{10} = \frac{2}{5} \).
Таким образом, окончательный ответ равен \( \frac{2}{5} \).
б) Выражение \( \frac{6}{1 — \frac{1}{3}} \) требует сначала вычислить знаменатель. Вычитаем \( \frac{1}{3} \) из 1, представленного как \( \frac{3}{3} \), получаем \( \frac{3}{3} — \frac{1}{3} = \frac{2}{3} \). Теперь знаменатель равен \( \frac{2}{3} \).
Деление на дробь эквивалентно умножению на её обратную, поэтому \( \frac{6}{\frac{2}{3}} = 6 \times \frac{3}{2} \). Умножаем: \( 6 \times \frac{3}{2} = \frac{6 \times 3}{2} = \frac{18}{2} \). Сокращаем: \( \frac{18}{2} = 9 \).
Итоговое значение равно 9.
в) Рассмотрим выражение \( \frac{\frac{2}{3} + \frac{1}{6}}{3} \). Сначала складываем дроби в числителе. Для этого приводим их к общему знаменателю 6: \( \frac{2}{3} = \frac{4}{6} \), затем \( \frac{4}{6} + \frac{1}{6} = \frac{5}{6} \).
Теперь делим \( \frac{5}{6} \) на 3, что равносильно умножению на обратное число: \( \frac{5}{6} \times \frac{1}{3} = \frac{5 \times 1}{6 \times 3} = \frac{5}{18} \).
Ответ: \( \frac{5}{18} \).
г) Вычислим \( \frac{1 — \frac{1}{6}}{2 + \frac{1}{6}} \). В числителе: \( 1 — \frac{1}{6} = \frac{6}{6} — \frac{1}{6} = \frac{5}{6} \). В знаменателе: \( 2 + \frac{1}{6} = \frac{12}{6} + \frac{1}{6} = \frac{13}{6} \).
Деление двух дробей равно умножению первой на обратную вторую: \( \frac{5}{6} \times \frac{6}{13} = \frac{5 \times 6}{6 \times 13} \). Сокращаем шестерки: \( \frac{5}{13} \).
Итог: \( \frac{5}{13} \).
д) Рассмотрим \( \frac{\frac{17}{100} — \frac{1}{10}}{10} \). Сначала вычитаем в числителе: \( \frac{1}{10} = \frac{10}{100} \), тогда \( \frac{17}{100} — \frac{10}{100} = \frac{7}{100} \).
Теперь делим \( \frac{7}{100} \) на 10, что равно умножению на \( \frac{1}{10} \): \( \frac{7}{100} \times \frac{1}{10} = \frac{7}{1000} \).
Ответ: \( \frac{7}{1000} \).
е) Вычислим \( \frac{\frac{1}{4} + \frac{2}{3}}{2 — \frac{1}{6}} \). Сложим числитель: приводим к общему знаменателю 12, \( \frac{1}{4} = \frac{3}{12} \), \( \frac{2}{3} = \frac{8}{12} \), сумма \( \frac{3}{12} + \frac{8}{12} = \frac{11}{12} \).
В знаменателе: \( 2 — \frac{1}{6} = \frac{12}{6} — \frac{1}{6} = \frac{11}{6} \).
Деление равно умножению числителя на обратную дробь знаменателя: \( \frac{11}{12} \times \frac{6}{11} = \frac{11 \times 6}{12 \times 11} \). Сокращаем 11: \( \frac{6}{12} = \frac{1}{2} \).
Итог: \( \frac{1}{2} \).


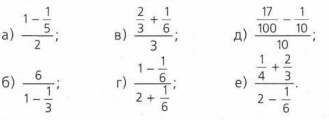


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!