Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 444 Дорофеев, Шарыгин — Подробные Ответы
а) Вылепите из пластилина цилиндр и разрежьте его так, чтобы в сечении получился круг; эллипс. Как надо разрезать цилиндр, чтобы в сечении получился прямоугольник?
б) Вылепите из пластилина конус. Разрежьте его так, чтобы в сечении получился эллипс. Как надо разрезать конус, чтобы в сечении получить треугольник? круг?
а) Чтобы в сечении получился круг, нужно разрезать цилиндр так, как показано на рисунке 5.20 (а) в учебнике.
Чтобы в сечении получился эллипс, нужно разрезать цилиндр так, как показано на рисунке 5.20 (б) в учебнике.
Чтобы в сечении получился прямоугольник, нужно разрезать цилиндр вдоль высоты:
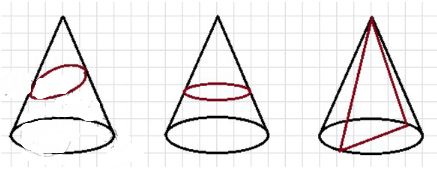
б) Разрежем конус так, чтобы в сечении получился эллипс, треугольник, круг:
Подробное объяснение способов разрезания цилиндра и конуса для получения различных сечений:
а) Разрезание цилиндра:
Чтобы в сечении цилиндра получить круг, нужно разрезать цилиндр перпендикулярно его оси, то есть горизонтальным сечением. Это показано на рисунке 5.20 (а) в учебнике. Такой срез проходит параллельно основанию цилиндра, и сечение совпадает с формой основания — кругом.
Чтобы получить эллипс в сечении цилиндра, нужно сделать разрез под углом к оси цилиндра, не перпендикулярно и не параллельно основанию. Это изображено на рисунке 5.20 (б). Такой наклонный срез приводит к эллиптической форме сечения.
Чтобы получить прямоугольник в сечении цилиндра, разрез необходимо сделать вдоль высоты цилиндра, то есть вертикальным сечением, проходящим через ось. На рисунке это показано красной линией, проходящей вдоль цилиндра. Такой разрез раскроет боковую поверхность цилиндра в виде прямоугольника.
б) Разрезание конуса:
Для конуса можно получить различные формы сечений в зависимости от направления разреза:
- Эллипс — разрез делается под углом к оси конуса, не перпендикулярно и не проходя через вершину.
- Треугольник — сечение получается, если разрез проходит через вершину конуса и пересекает основание.
- Круг — если разрезать конус плоскостью, параллельной основанию.
Эти построения помогают визуализировать и понять, как меняется форма сечения в зависимости от направления разреза, что важно для изучения свойств тел вращения и анализа геометрических фигур.
