Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 437 Дорофеев, Шарыгин — Подробные Ответы
Ищем способ построения.
Постройте треугольник по элементам, указанным на рисунке 5.13, а, б.
Примеры построения треугольников с высотой и углом:
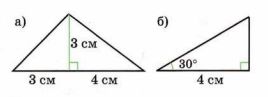
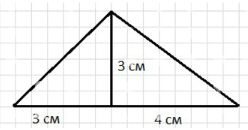
а) Построение треугольника с основанием 3 см и 4 см и высотой 3 см:
- Чертим основание треугольника длиной 3 см и 4 см (сумма двух частей основания).
- Проводим высоту, равную 3 см, от вершины к основанию.
- Соединяем концы основания с вершиной, чтобы получить треугольник.
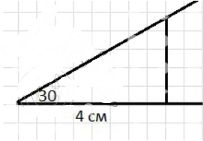
б) Построение треугольника с углом 30° и основанием 4 см:
- Рисуем угол в 30 градусов с помощью транспортира.
- Отмеряем на одной стороне угла основание длиной 4 см.
- Проводим высоту из вершины угла перпендикулярно основанию.
Подробное описание примеров построения треугольников с заданными параметрами:
а) Построение треугольника с основанием 3 см и 4 см и высотой 3 см:
Для начала чертим основание треугольника, которое состоит из двух частей длиной 3 см и 4 см. Эти отрезки можно отметить на одной линии, суммарно это будет 7 см.
Далее проводим высоту треугольника — перпендикуляр из вершины к основанию — длиной 3 см. Это позволяет определить высоту, необходимую для расчётов площади или других характеристик треугольника.
После этого соединяем концы основания с вершиной, получая полный треугольник. Такой подход позволяет визуально и геометрически понять расположение высоты и её связь с основанием.
б) Построение треугольника с углом 30° и основанием 4 см:
Сначала с помощью транспортира чертим угол, равный 30 градусам. Это будет один из углов треугольника.
Затем на одной стороне угла откладываем основание длиной 4 см. Это фиксирует длину одной из сторон треугольника.
После этого из вершины угла проводим высоту — перпендикуляр, опущенный на основание. Это позволяет получить полный треугольник и подготовиться к дальнейшим вычислениям, например, нахождению площади или других параметров.
Значение построений:
Такие построения важны для изучения свойств треугольников и практического применения геометрических понятий. Чёткое измерение и построение высоты, углов и оснований помогает в дальнейшем решении задач на вычисление площади, периметра, определения типов треугольников и других геометрических характеристик.
Рекомендации:
- Используйте транспортир для точного измерения углов.
- Применяйте линейку для точного отмеривания длин сторон.
- Обязательно проводите высоты перпендикулярно основанию для правильного построения.
- Соблюдайте аккуратность в черчении, чтобы получить правильные и точные фигуры.
