ГДЗ по Математике 6 Класс Номер 436 Дорофеев, Шарыгин — Подробные Ответы

Ищем закономерность.
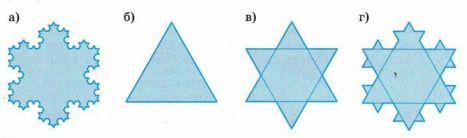
Многоугольник, изображённый на рисунке 5.12, а, называют снежинкой Коха. Постройте её по следующему алгоритму:
• начертите на листе нелинованной бумаги равносторонний треугольник со стороной 9 см (рис. 5.12, б);
• каждую сторону треугольника разделите на 3 равные части и на средней части постройте равносторонний треугольник (рис. 5.12, в);
• повторите это построение на каждой из 12 сторон получившегося многоугольника (рис. 5.12, г);
• чтобы получить снежинку, изображённую на рисунке 5.12, а, надо сделать ещё один шаг построения.
Во сколько раз увеличивается число сторон снежинки Коха на каждом шаге построения? Во сколько раз при этом уменьшается длина её стороны? Сколько сторон у снежинки, получаемой на каждом шаге? Чему равен её периметр?

Выполните построения сами.
Число сторон снежинки Коха на каждом шаге увеличивается в 4 раза, так как было три стороны, стало 12 сторон. Под буквой г) уже имеет 48 сторон (12 × 4 = 48).
Длина стороны при этом уменьшается в 3 раза.
Сначала у снежинки было 3 стороны, затем стало 12, после — 48, далее — 192 стороны.
Периметр снежинки на последнем шаге будет равен
если длина стороны стала равна \( \frac{1}{3} \) см:
\( 192 \times \frac{1}{3} = 64 \) см.

Число сторон снежинки Коха увеличивается в 4 раза на каждом шаге, так как каждый отрезок заменяется четырьмя новыми. Изначально у фигуры было 3 стороны, затем после первого шага стало \( 3 \times 4 = 12 \) сторон. На следующем шаге количество сторон увеличилось до \( 12 \times 4 = 48 \), а потом до \( 48 \times 4 = 192 \). Таким образом, количество сторон на каждом шаге растет по формуле \( 3 \times 4^n \), где \( n \) — номер шага.

При этом длина каждой стороны уменьшается в 3 раза на каждом шаге. Если изначальная длина стороны была \( L \), то после первого шага длина станет \( \frac{L}{3} \), после второго — \( \frac{L}{3^2} \), после третьего — \( \frac{L}{3^3} \) и так далее. Это связано с тем, что каждый отрезок разбивается на три части, и средняя часть заменяется на два новых отрезка, суммарная длина которых равна одной трети от исходной.

Периметр снежинки на последнем шаге равен произведению количества сторон на длину одной стороны. На последнем шаге число сторон равно 192, а длина стороны стала \( \frac{1}{3} \) см. Тогда периметр будет равен \( 192 \times \frac{1}{3} = 64 \) см. Это показывает, что несмотря на уменьшение длины стороны, общее число сторон растет так быстро, что периметр увеличивается.