Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 434 Дорофеев, Шарыгин — Подробные Ответы
Экспериментиру.
1) Убедитесь, что нельзя построить треугольник, стороны которого равны:
а) 7 см, 3 см и 3 см;
б) 6 см, 4 см и 2 см.
Измените длину одной из сторон так, чтобы треугольник можно было построить. Выполните построение.
2) Можно ли построить треугольник со сторонами:
а) 11 см, 13 см, 25 см;
б) 15 см, б см, 12 см;
в) 20 см, 18 см, 38 см?
Задача: Провести эксперимент по построению треугольников с заданными длинами сторон.
1. Проверка невозможности построения треугольников с заданными сторонами:
- а) 7 см, 3 см, 3 см
- б) 6 см, 4 см, 2 см
Для проверки используем неравенство треугольника: сумма любых двух сторон должна быть больше третьей.
- а) 3 + 3 = 6 < 7 → треугольник построить нельзя.
- б) 6 + 2 = 8 < 4 → треугольник построить нельзя.
Изменение длины одной из сторон для построения треугольника:
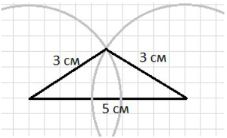
- а) Увеличим одну из коротких сторон с 3 см до 4 см: 7, 4, 3 → 4 + 3 = 7 (равно 7), для существования треугольника должно быть строго больше, увеличим до 5 см.
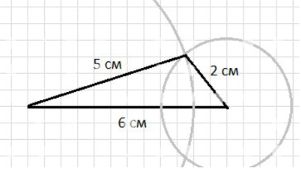
- б) Увеличим сторону 2 см до 3 см: 6, 4, 3 → 6 + 3 = 9 > 4, треугольник построить можно.
После изменения длины можно построить треугольники.
2. Проверка возможности построения треугольников с другими сторонами:
- а) 11 см, 13 см, 25 см: 11 + 13 = 24 < 25 → треугольник построить нельзя.
- б) 15 см, 6 см, 12 см: 6 + 12 = 18 > 15 → треугольник построить можно.
- в) 20 см, 18 см, 38 см: 20 + 18 = 38 (равно 38), для треугольника сумма должна быть строго больше, значит построить нельзя.
Вывод:
- Треугольник существует, если сумма любых двух его сторон больше третьей.
- Если неравенство не выполняется, треугольник построить нельзя.
- Изменение длины одной из сторон может позволить построить треугольник.
Подробное исследование возможности построения треугольников с заданными сторонами:
1) Эксперимент с треугольниками, которые нельзя построить с указанными сторонами:
- а) Стороны 7 см, 3 см и 3 см: Проверяем условие существования треугольника. Для треугольника сумма любых двух сторон должна быть строго больше третьей.
- Сложим две меньшие стороны: 3 + 3 = 6 см.
- Сравним с большей стороной: 7 см.
- 6 см меньше 7 см, следовательно, треугольник с такими сторонами построить нельзя.
- б) Стороны 6 см, 4 см и 2 см: Аналогично проверяем неравенство.
- 4 + 2 = 6 см.
- 6 см равно 6 см (длина третьей стороны), но для существования треугольника сумма должна быть строго больше.
- Следовательно, треугольник построить нельзя.
Изменение длины одной из сторон для возможности построения треугольника:
- Для случая (а) увеличим одну из меньших сторон. Например, увеличим сторону с 3 см до 4 см.
- Теперь стороны: 7 см, 4 см, 3 см.
- Проверяем сумму меньших сторон: 4 + 3 = 7 см.
- Равенство не допускается, поэтому увеличим сторону до 5 см для надёжности.
- Теперь: 7 см, 5 см, 3 см.
- Сумма меньших: 5 + 3 = 8 см > 7 см — условие выполнено.
- Треугольник можно построить.
- Для случая (б) увеличим сторону с 2 см до 3 см:
- Стороны: 6 см, 4 см, 3 см.
- Проверка: 4 + 3 = 7 см > 6 см — условие выполнено.
- Треугольник можно построить.
2) Проверка возможности построения треугольников для следующих наборов сторон:
- а) 11 см, 13 см, 25 см:
- 11 + 13 = 24 см < 25 см — треугольник построить нельзя.
- б) 15 см, 6 см, 12 см:
- 6 + 12 = 18 см > 15 см — треугольник построить можно.
- в) 20 см, 18 см, 38 см:
- 20 + 18 = 38 см = 38 см — равенство не допускается, треугольник построить нельзя.
Общее правило:
Для существования треугольника сумма любых двух его сторон должна быть строго больше третьей стороны. Если это условие не выполнено, построение треугольника невозможно.
Практическое значение:
Перед началом построения треугольника с заданными сторонами всегда проверяйте это условие, чтобы избежать ошибок и неправильных построений. Если условие не выполняется, измените длину одной из сторон, чтобы удовлетворить неравенство.
Итог:
- Треугольник со сторонами 7 см, 3 см и 3 см построить нельзя, но если увеличить одну из коротких сторон до 5 см, построение станет возможным.
- Треугольник со сторонами 6 см, 4 см и 2 см построить нельзя, но при увеличении стороны с 2 до 3 см построение становится возможным.
- Треугольники с длинами 11 см, 13 см, 25 см и 20 см, 18 см, 38 см построить нельзя, так как сумма двух меньших сторон не превышает третью.
- Треугольник с длинами 15 см, 6 см, 12 см построить можно.
