Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 433 Дорофеев, Шарыгин — Подробные Ответы
Действуем по алгоритму.
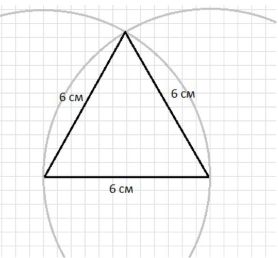
а) Постройте равносторонний треугольник со стороной б см.
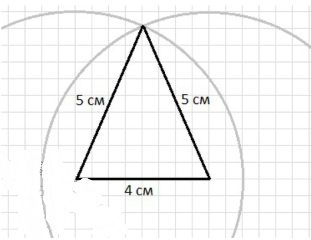
б) Постройте равнобедренный треугольник, основание которого равно 4 см, а боковые стороны — 5 см.
Пример построения треугольников по заданным параметрам:
а) Равносторонний треугольник со стороной 6 см:
- Начертите основание длиной 6 см.
- Проведите две дуги окружностей с радиусом 6 см, центры которых расположены в концах основания.
- Точка пересечения дуг — вершина треугольника.
- Соедините вершину с концами основания — получится равносторонний треугольник.
б) Равнобедренный треугольник с основанием 4 см и боковыми сторонами по 5 см:
- Начертите основание длиной 4 см.
- Проведите дуги окружностей радиусом 5 см с центрами в концах основания.
- Точка пересечения дуг — вершина треугольника.
- Соедините вершину с концами основания — получите равнобедренный треугольник.
На рисунках видно, что длины сторон соответствуют указанным размерам, а построения выполнены с помощью циркуля и линейки для точного измерения.
Подробное описание построения треугольников по заданным параметрам с примерами:
а) Равносторонний треугольник со стороной 6 см:
Для построения равностороннего треугольника необходимо, чтобы все три стороны были равны. В нашем случае длина каждой стороны — 6 см.
- С помощью линейки начертите отрезок длиной ровно 6 см. Это будет основание треугольника.
- Возьмите циркуль и установите его радиус равным 6 см, то есть равным длине основания.
- Поставьте иглу циркуля на один конец отрезка основания и проведите дугу.
- Не меняя радиуса циркуля, поставьте иглу на другой конец основания и проведите вторую дугу, пересекающую первую.
- Точка пересечения двух дуг — вершина треугольника, которую нужно соединить с концами основания.
В итоге получится равносторонний треугольник, в котором каждая сторона равна 6 см, как показано на рисунке.
б) Равнобедренный треугольник с основанием 4 см и боковыми сторонами по 5 см:
Для построения равнобедренного треугольника необходимо, чтобы две стороны были равны — в данном случае боковые стороны равны 5 см, а основание — 4 см.
- С помощью линейки начертите отрезок длиной 4 см — это будет основание треугольника.
- Установите радиус циркуля равным 5 см, что соответствует длине боковых сторон.
- Поставьте иглу циркуля на один конец основания и проведите дугу.
- Поставьте иглу циркуля на другой конец основания и проведите вторую дугу, которая пересечёт первую.
- Точка пересечения дуг — вершина треугольника. Соедините эту точку с концами основания.
В результате получится равнобедренный треугольник с основанием 4 см и боковыми сторонами 5 см, как показано на рисунке.
Заключение:
Такое построение с помощью циркуля и линейки — классический способ точного построения треугольников с заданными сторонами. Пересечение дуг окружностей, радиусы которых равны длинам боковых сторон, гарантирует точность построения и равенство соответствующих сторон треугольника.
