Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 432 Дорофеев, Шарыгин — Подробные Ответы
Отрезки, изображённые на рисунке 5.11, — стороны треугольника. Постройте этот треугольник.
Подробное объяснение построения треугольника по заданным сторонам:
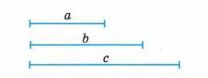
1. Измеряем отрезок c и чертим его в тетради. Этот отрезок будет основанием треугольника.
2. Рисуем окружность с центром в одном конце отрезка c и радиусом, равным длине отрезка a. Это задаёт расстояние до второй вершины треугольника от этой точки.
3. Рисуем вторую окружность с центром в другом конце отрезка c и радиусом, равным длине отрезка b. Эта окружность определяет возможные положения третьей вершины треугольника, соответствующей длине стороны b.
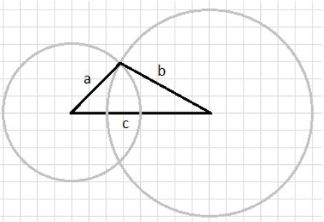
4. Точка пересечения этих двух окружностей является третьей вершиной треугольника. Соединяя эту точку с концами отрезка c, получаем треугольник с заданными сторонами a, b и c.
Итог: Данный способ построения позволяет точно воспроизвести треугольник по трём известным сторонам, используя циркуль и линейку, что гарантирует равенство построенной фигуры исходной.
Подробное пошаговое объяснение построения треугольника по трем сторонам a, b и c:
1. Сначала измеряем отрезок c, который будет основанием будущего треугольника, и аккуратно чертим его в тетради. Это основной отрезок, на котором будут построены остальные части фигуры.
2. Далее берём циркуль и ставим его иглу в одном конце отрезка c. Радиус циркуля устанавливаем равным длине отрезка a, которая соответствует одной из сторон треугольника, прилегающей к основанию.
3. С центром в этой точке (одном конце отрезка c) проводим дугу окружности. Эта дуга показывает все возможные положения вершины треугольника, расстояние от которой до центра равно длине a.
4. Аналогично, ставим иглу циркуля в другой конец отрезка c и устанавливаем радиус равным длине отрезка b, второй стороне треугольника, прилегающей к основанию с другой стороны.
5. Проводим вторую дугу окружности с этим радиусом. Место пересечения двух дуг — это точка, которая будет третьей вершиной треугольника.
6. Соединяем точку пересечения дуг с концами отрезка c. В результате получаем треугольник, все стороны которого равны заданным отрезкам a, b и c.
Почему этот метод работает:
Поскольку каждая дуга описывает множество точек на заданном расстоянии от центра, пересечение двух дуг соответствует точке, удалённой от концов основания на длины, равные a и b. Таким образом, треугольник с требуемыми сторонами точно воспроизводится.
Вывод: Использование циркуля и линейки для построения по трем сторонам — классический и надёжный способ построения треугольников, который гарантирует точность и равенство построенной фигуры исходной.
