Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 431 Дорофеев, Шарыгин — Подробные Ответы
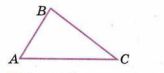
Постройте треугольник, равный треугольнику АВС (рис. 5.10).
Указание. Стороны треугольника измеряйте циркулем.
Пояснение к построению равного треугольника ABC:
1. Измеряем отрезок AC и чертим его в тетради.
2. Рисуем окружность с центром в точке A и радиусом, равным длине отрезка AB.
3. Рисуем окружность с центром в точке C и радиусом, равным длине отрезка BC.
4. Точка пересечения этих двух окружностей является точкой B.
Таким образом, соединяя точки A, B и C, получаем треугольник, равный исходному треугольнику ABC.
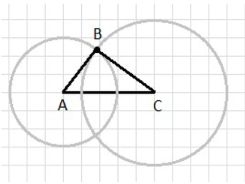
Подробное объяснение построения равного треугольника ABC по заданному рисунку:
1. Для начала измеряем длину отрезка AC, используя линейку или циркуль. Этот отрезок нужно аккуратно перенести и начертить в тетради. Отрезок AC будет основой будущего треугольника.
2. Далее с помощью циркуля рисуем окружность с центром в точке A. Радиус этой окружности должен быть равен длине отрезка AB, то есть расстоянию от точки A до точки B исходного треугольника.
3. Затем рисуем вторую окружность с центром в точке C, радиус которой равен длине отрезка BC. Это значит, что радиус равен расстоянию между точками B и C в исходном треугольнике.
4. Точка пересечения этих двух окружностей будет точкой B. Именно эта точка позволяет воспроизвести углы и стороны треугольника, гарантируя равенство построенного треугольника исходному.
5. После нахождения точки B соединяем её с точками A и C прямыми линиями. В результате получаем треугольник ABC, который полностью равен исходному треугольнику, поскольку все стороны имеют равные длины.
Заключение: Такой способ построения называется построением по трём сторонам (SSS). Использование циркуля и точных измерений гарантирует точное копирование треугольника. Это один из классических приёмов в геометрии, который позволяет переносить фигуры с сохранением их размеров и формы.
