Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 426 Дорофеев, Шарыгин — Подробные Ответы
Найдите периметр четырёхугольника ABCD (рис. 5.7; сторона одной клетки равна 5 мм).
Так как окружность с центром в точке A имеет радиус, равный 1 см, то отрезки AB и AD равны по 1 см.
Так как окружность с центром в точке C имеет радиус, равный 1,5 см, то отрезки BC и CD равны по 1,5 см.
Периметр четырёхугольника ABCD равен:
AB + BC + CD + AD = 1 + 1,5 + 1,5 + 1 = 2,5 + 2,5 = 5 (см).
Ответ: 5 см.
Рассмотрим подробно решение задачи по нахождению периметра четырёхугольника ABCD.
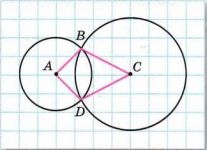
1. На рисунке изображены две окружности. Первая окружность с центром в точке A имеет радиус, равный 1 см, вторая окружность с центром в точке C — радиус 1,5 см.
2. Из условия и рисунка видно, что отрезки AB и AD являются радиусами окружности с центром в точке A. Следовательно, эти отрезки равны 1 см каждый.
3. Аналогично, отрезки BC и CD являются радиусами окружности с центром в точке C, значит их длина равна 1,5 см каждый.
4. Периметр четырёхугольника ABCD — это сумма длин всех его сторон:
Периметр = AB + BC + CD + AD
Подставляем значения:
Периметр = 1 + 1,5 + 1,5 + 1 = 2 + 3 = 5 см.
5. Таким образом, периметр четырёхугольника ABCD равен 5 см.
Вывод: благодаря свойствам радиусов окружностей, равенство соответствующих отрезков позволяет легко вычислить периметр четырёхугольника, используя простое сложение.
