Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 424 Дорофеев, Шарыгин — Подробные Ответы
Экспериментируем.
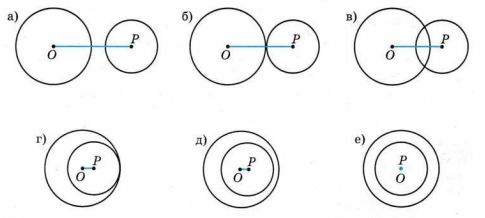
Для каждого случая взаимного расположения двух окружностей (см. рис. 5.4) определите, сколько можно провести различных прямых, касающихся обеих окружностей. Сделайте в тетради схематические рисунки.
Задача: Определить количество различных прямых, касающихся двух окружностей для каждого случая взаимного расположения (рис. 5.4), и сделать схематические рисунки.
Анализ и ответ для каждого случая:
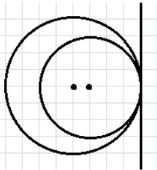
1. Случай а) — две окружности не пересекаются и не касаются:
Можно провести 4 касательные прямые: 2 внешние и 2 внутренние касательные.
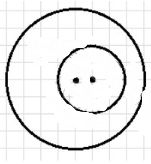
2. Случай б) — две окружности касаются внешним образом:
Можно провести 3 касательные прямые: 2 внешние и 1 внутренняя касательная, проходящая через точку касания.
3. Случай в) — две окружности пересекаются в двух точках:
Можно провести 2 касательные прямые: 2 внешние касательные.
4. Случай г) — одна окружность лежит внутри другой, но не касаются:
Можно провести 1 касательную прямую — внешнюю касательную, касающуюся обеих окружностей.
5. Случай д) — одна окружность лежит внутри другой, касаясь её внутренним образом:
Можно провести 1 касательную прямую — касательную в точке внутреннего касания.
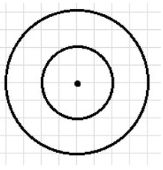
6. Случай е) — одна окружность лежит внутри другой и не касаются:
Касательных прямых, касающихся обеих окружностей, нет.
Рекомендация: В тетради сделайте схематические рисунки для каждого случая, изображая окружности и соответствующие касательные прямые.
Задача: Для каждого случая взаимного расположения двух окружностей (см. рис. 5.4) определить количество различных прямых, которые касаются обеих окружностей, и сделать схематические рисунки в тетради.
Общее понимание: Прямая, касающаяся окружности, называется касательной к этой окружности. Для двух окружностей существует несколько касательных, которые могут касаться одновременно обеих окружностей. Количество таких касательных зависит от взаимного расположения окружностей.
Анализ каждого случая:
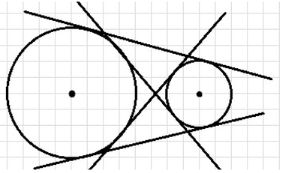
1. Случай а) — две окружности лежат отдельно, не пересекаются и не касаются друг друга.
В этом случае существует 4 различных касательных прямых, которые касаются обеих окружностей:
- Две внешние касательные — проходят вне двух окружностей, касаясь их снаружи.
- Две внутренние касательные — проходят между окружностями, касаясь их с внутренней стороны.
Таким образом, всего 4 касательных прямых.
2. Случай б) — две окружности касаются друг друга внешним образом.
В этом случае количество касательных уменьшается до 3:
- Две внешние касательные, как и в случае (а).
- Одна внутренняя касательная — проходящая через точку касания окружностей.
Всего 3 касательные прямые.
3. Случай в) — две окружности пересекаются в двух точках.
В этом случае существует только 2 внешние касательные прямые, касающиеся обеих окружностей.
Внутренних касательных прямых, касающихся обеих окружностей, нет, так как окружности пересекаются.
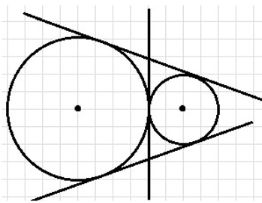
4. Случай г) — одна окружность лежит внутри другой, но они не касаются друг друга.
Здесь количество общих касательных прямых сокращается до 1:
- Существует одна внешняя касательная, которая касается обеих окружностей.
Внутренних касательных нет, так как окружности не пересекаются и не касаются.
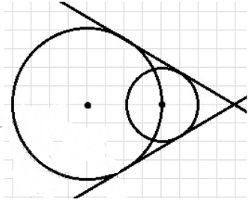
5. Случай д) — одна окружность лежит внутри другой, касаясь её внутренним образом.
Здесь возможна только одна касательная прямая — внутренняя касательная, проходящая через точку касания внутри.
Общие внешние касательные отсутствуют.
6. Случай е) — одна окружность полностью лежит внутри другой, не касаясь её.
В этом случае касательных прямых, касающихся обеих окружностей, не существует.
Итоговая таблица:
| Случай | Взаимное расположение окружностей | Количество касательных прямых |
|---|---|---|
| а) | Окружности лежат отдельно | 4 |
| б) | Окружности касаются внешним образом | 3 |
| в) | Окружности пересекаются | 2 |
| г) | Одна окружность внутри другой, не касаются | 1 |
| д) | Одна окружность внутри другой, касаются внутренним образом | 1 |
| е) | Одна окружность внутри другой, не касаются | 0 |
Рекомендации для выполнения задания в тетради:
- Для каждого случая нарисуйте схематически две окружности в соответствии с изображением на рис. 5.4.
- Отметьте и проведите все возможные касательные прямые, касающиеся обеих окружностей.
- Подпишите количество касательных и их тип (внутренние или внешние).
Такой подход поможет лучше понять взаимное расположение окружностей и свойства касательных прямых к ним.
