Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 423 Дорофеев, Шарыгин — Подробные Ответы
Ищем способ построения. Постройте цветок, изображённый на рисунке 5.5.
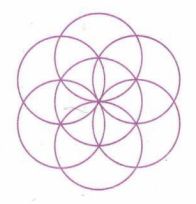
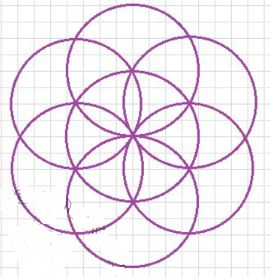
Задача: Построить «цветок», изображённый на рисунке (7 окружностей одинакового радиуса, расположенных так, что одна центральная окружность окружена шестью окружностями, касающимися её и соседних окружностей).
Решение:
1. Начертите центральную окружность радиусом R.
2. Вокруг неё начертите шесть окружностей того же радиуса R так, чтобы каждая касалась центральной и двух соседних окружностей.
3. Центры внешних окружностей расположены на вершинах правильного шестиугольника с длиной стороны R, вписанного в окружность с центром в центре цветка.
Пояснение с координатами (если строить в системе координат):
- Центр центральной окружности: (0, 0)
- Центры шести окружностей вокруг расположены под углами 0°, 60°, 120°, 180°, 240°, 300°, на расстоянии R от центра
Задача: Построить фигуру в виде «цветка», состоящую из семи окружностей одинакового радиуса, где одна окружность расположена в центре, а шесть остальных касаются центральной и соседних окружностей, образуя правильный узор.
Объяснение: Такая фигура строится на основе геометрической фигуры — правильного шестиугольника, вписанного в окружность. Центры шести внешних окружностей расположены на вершинах этого правильного шестиугольника вокруг центральной окружности.
Пошаговое построение:
- Начертите центральную окружность с радиусом \( R \). Это будет центр «цветка».
- Определите центры шести окружностей, которые будут окружать центральную. Они должны лежать на окружности радиуса \( R \) вокруг центра центральной окружности.
- Расположите центры этих шести окружностей под углами: 0°, 60°, 120°, 180°, 240°, 300° относительно центра.
- Нарисуйте каждую из шести окружностей с радиусом \( R \), используя найденные центры.
- Убедитесь, что каждая внешняя окружность касается центральной окружности и двух соседних внешних окружностей.
Математические детали:
Для радиуса окружностей \( R \) координаты центров внешних окружностей рассчитываются так:
