Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 420 Дорофеев, Шарыгин — Подробные Ответы
В таблице приведены расстояние ОА между центрами двух окружностей и их радиусы R и r. Постройте эти окружности. В каждом случае найдите расстояние между самыми удалёнными и самыми близкими точками окружностей.
ОА , см 0,5 1 6 5 2
R, см 3 4 2 3 2,5
r, см 2 3 2 2 2
Анализ взаимного расположения двух окружностей по примерам:
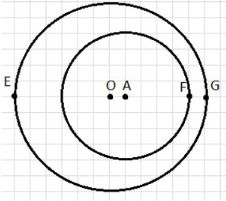
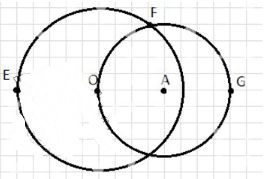
1. Окружность с радиусами R=3 см и r=2 см, расстояние между центрами OA=0,5 см.
Расстояние между ближайшими точками (FG) = 0,5 см.
Расстояние между удалёнными точками (EF) = 5,5 см.
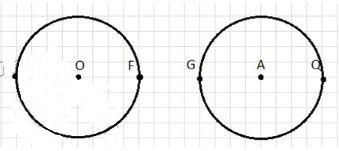
2. Окружность с радиусами R=4 см и r=3 см, расстояние между центрами OA=1 см.
Расстояние между ближайшими точками (FG) = 0 см (окружности касаются).
Расстояние между удалёнными точками (EF) = 8 см.
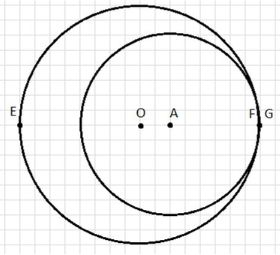
3. Окружность с радиусами R=6 см и r=2 см, расстояние между центрами OA=6 см.
Расстояние между ближайшими точками (FG) = 2 см.
Расстояние между удалёнными точками (EF) = 10 см.
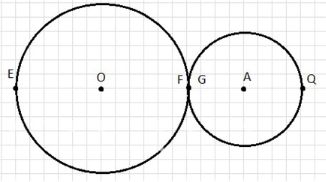
4. Окружность с радиусами R=3 см и r=2 см, расстояние между центрами OA=5 см.
Расстояние между ближайшими точками (FG) = 0 см (окружности касаются).
Расстояние между удалёнными точками (EF) = 10 см.
5. Окружность с радиусами R=2,5 см и r=2 см, расстояние между центрами OA=1 см.
Расстояние между ближайшими точками (FG) = 0 см (окружности касаются).
Расстояние между удалёнными точками (EF) = 6,5 см.
Выводы:
- Если расстояние между центрами меньше суммы радиусов, окружности пересекаются.
- Если расстояние между центрами равно сумме радиусов, окружности касаются.
- Расстояние между ближайшими точками FG показывает расстояние между касательными или точками пересечения.
- Расстояние между удалёнными точками EF — максимальное расстояние между точками окружностей.
Подробный анализ взаимного расположения двух окружностей на основе приведённых примеров:
1. В первом примере даны две окружности с радиусами R = 3 см и r = 2 см, а расстояние между центрами окружностей OA равно 0,5 см.
Значение расстояния между ближайшими точками окружностей (обозначено как FG) составляет 0,5 см.
Расстояние между самыми удалёнными точками окружностей (обозначено как EF) равно 5,5 см.
Поскольку расстояние между центрами меньше суммы радиусов (0,5 см < 3 + 2 = 5 см), окружности пересекаются.
2. Во втором примере радиусы окружностей равны R = 4 см и r = 3 см, а расстояние между центрами OA равно 1 см.
Расстояние между ближайшими точками (FG) равно 0 см, что указывает на касание окружностей.
Расстояние между удалёнными точками (EF) равно 8 см.
Значит, окружности касаются друг друга в одной точке, поскольку расстояние между центрами равно сумме радиусов (1 см = 4 − 3).
3. В третьем примере радиусы составляют R = 6 см и r = 2 см, расстояние между центрами OA — 6 см.
Расстояние между ближайшими точками окружностей (FG) равно 2 см.
Расстояние между удалёнными точками (EF) равно 10 см.
Поскольку расстояние между центрами больше разности радиусов, но меньше суммы радиусов (2 см < 6 см < 8 см), окружности пересекаются.
4. Четвёртый пример — окружности с радиусами R = 3 см и r = 2 см, расстояние между центрами OA равно 5 см.
Расстояние между ближайшими точками (FG) равно 0 см, что означает касание окружностей.
Расстояние между удалёнными точками (EF) равно 10 см.
Окружности касаются внешним образом, так как расстояние между центрами равно сумме радиусов (5 см = 3 + 2).
5. В пятом примере радиусы равны R = 2,5 см и r = 2 см, расстояние между центрами OA равно 1 см.
Расстояние между ближайшими точками (FG) равно 0 см — окружности касаются.
Расстояние между удалёнными точками (EF) равно 6,5 см.
Здесь окружности касаются внутренним образом, так как расстояние между центрами равно разности радиусов (1 см = 2,5 − 2).
Общие выводы по взаимному расположению окружностей:
- Если расстояние между центрами окружностей меньше суммы их радиусов и больше их разности, окружности пересекаются в двух точках.
- Если расстояние между центрами равно сумме радиусов, окружности касаются внешним образом в одной точке.
- Если расстояние между центрами равно разности радиусов, окружности касаются внутренним образом.
- Расстояние между ближайшими точками (FG) показывает, насколько близко расположены окружности, включая случаи касания (FG = 0) и пересечения.
- Расстояние между удалёнными точками (EF) показывает максимальное расстояние между точками окружностей, полезное для понимания их взаимного расположения в пространстве.
Таким образом, анализируя расстояния между центрами и радиусы окружностей, можно точно определить, касаются ли они, пересекаются или не имеют общих точек.
