ГДЗ по Математике 6 Класс Номер 419 Дорофеев, Шарыгин — Подробные Ответы
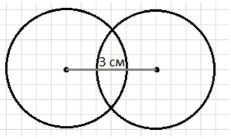
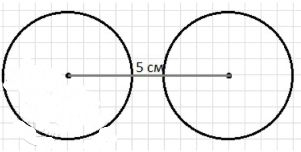
Начертите две равные окружности так, чтобы они: пересекались; не пересекались. В каждом случае измерьте расстояние между центрами окружностей.
Построение двух равных окружностей и измерение расстояния между их центрами в разных случаях:
1. Пересекающиеся окружности:
- Начертите две окружности одинакового радиуса так, чтобы они частично перекрывали друг друга — пересекались в двух точках.
- Измерьте расстояние между центрами этих окружностей. Это расстояние будет меньше суммы их радиусов и больше их разности.
- То есть, если радиус каждой окружности равен R, то расстояние между центрами d удовлетворяет условию:
0 < d < 2R
2. Непересекающиеся окружности:
- Начертите две равные окружности с таким расположением, чтобы они не касались и не пересекались.
- Измерьте расстояние между центрами окружностей.
- В этом случае расстояние между центрами будет больше суммы их радиусов:
d > 2R
Итог: расстояние между центрами двух равных окружностей определяет их взаимное расположение — пересечение или отсутствие пересечения.
Подробное руководство по построению двух равных окружностей и измерению расстояния между их центрами в различных случаях:
1. Пересекающиеся окружности:
- Для начала возьмите циркуль и настройте его так, чтобы радиус окружности был определён и одинаков для обеих окружностей.
- Начертите первую окружность на листе бумаги, обозначьте её центр точкой O₁.
- Выберите точку O₂, расположенную так, чтобы расстояние между O₁ и O₂ было меньше суммы радиусов, но больше их разности. Это обеспечит частичное перекрытие окружностей.
- Постройте вторую окружность с тем же радиусом вокруг точки O₂.
- Окружности пересекутся в двух точках, которые можно обозначить как точки пересечения.
- Измерьте расстояние между центрами окружностей O₁ и O₂ линейкой или другим измерительным инструментом.
- Это расстояние d удовлетворяет условию: 0 < d < 2R, где R — радиус окружностей.
2. Непересекающиеся окружности:
- Повторите шаги с циркулем, установив тот же радиус для окружностей.
- Начертите первую окружность с центром O₁.
- Выберите точку O₂ так, чтобы расстояние между центрами O₁ и O₂ было больше суммы радиусов окружностей (d > 2R).
- Постройте вторую окружность вокруг точки O₂ с тем же радиусом.
- В этом случае окружности не будут пересекаться и не будут касаться друг друга.
- Измерьте расстояние между центрами окружностей.
Дополнительные пояснения:
- Если расстояние между центрами двух равных окружностей равно сумме их радиусов (d = 2R), то окружности касаются друг друга в одной точке (касательные окружности).
- Если расстояние между центрами равно разности радиусов (для равных окружностей это 0), окружности совпадают полностью.
Вывод: положение двух равных окружностей относительно друг друга (пересекаются, не пересекаются или касаются) напрямую зависит от расстояния между их центрами по отношению к радиусу окружностей.
