Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 411 Дорофеев, Шарыгин — Подробные Ответы
Экспериментируем.
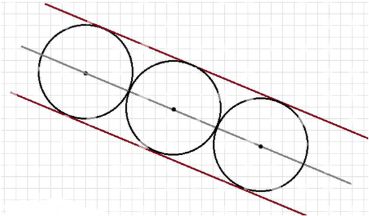
Начертите две параллельные прямые. Постройте какую-нибудь окружность, для которой обе эти прямые являются касательными. Сколько таких окружностей можно построить? Где лежат их центры?
Экспериментальное задание:
- Начертите на листе две параллельные прямые.
- Постройте окружность, которая касается обеих этих прямых.
Вопрос: Сколько таких окружностей можно построить? Где будут располагаться их центры?
Ответ:
Можно построить бесконечное множество окружностей, касающихся обеих параллельных прямых.
Это связано с тем, что центр любой такой окружности должен находиться на прямой, параллельной данным касательным и расположенной ровно посередине между ними — на линии, которая равноудалена от обеих прямых.
Расстояние между параллельными прямыми равно диаметру искомых окружностей, а радиус каждой окружности равен половине этого расстояния.
Таким образом, для любой точки на средней линии (между двумя параллельными прямыми) с расстоянием до каждой прямой, равным радиусу окружности, существует окружность, касающаяся обеих прямых.
Итог: центры таких окружностей лежат на средней линии, проходящей посередине между двумя параллельными прямыми, и расстояние между этими прямыми равно диаметру построенных окружностей.
Экспериментальное задание:
- На листе бумаги начертите две прямые, которые обязательно будут параллельны друг другу.
- Далее попробуйте построить окружность, для которой обе эти прямые будут касательными.
Вопрос: Сколько таких окружностей можно построить? Где расположены их центры?
Подробный ответ:
При построении окружности, касающейся двух параллельных прямых, необходимо учесть следующие геометрические свойства:
- Касательная к окружности — это прямая, которая касается окружности ровно в одной точке и при этом перпендикулярна радиусу, проведённому к точке касания.
- Если у нас есть две параллельные прямые, то расстояние между ними — это постоянная величина, которая будет связана с радиусом искомой окружности.
Для того чтобы окружность касалась обеих параллельных прямых, её радиус должен быть равен половине расстояния между этими прямыми.
Центр такой окружности будет лежать на прямой, которая проходит ровно посередине между двумя параллельными прямыми — на линии, равнодалёной от обеих.
Поскольку на этой средней линии можно выбрать бесконечное количество точек, каждая из которых будет центром окружности с радиусом, равным половине расстояния между прямыми, то можно построить бесконечно много таких окружностей.
Иными словами, для каждой точки на средней линии между двумя параллельными прямыми существует окружность, касающаяся обеих прямых, радиус которой равен половине расстояния между этими прямыми.
Итог:
- Количество окружностей, касающихся двух параллельных прямых, бесконечно.
- Центры этих окружностей располагаются на средней линии, проходящей между двумя параллельными прямыми.
- Радиус каждой окружности равен половине расстояния между этими прямыми.
