Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 409 Дорофеев, Шарыгин — Подробные Ответы
Действуем по алгоритму.
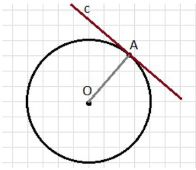
Начертите произвольную окружность и отметьте на ней точку А. Постройте касательную к окружности в точке А.
Алгоритм построения касательной к окружности в точке A:
- Начертите произвольную окружность с центром O.
- Отметьте на окружности точку A.
- Проведите радиус OA — от центра O до точки A.
- Постройте прямую, проходящую через точку A, перпендикулярную радиусу OA.
- Эта прямая будет касательной к окружности в точке A.
Обоснование: касательная к окружности в точке касания перпендикулярна радиусу, проведённому в эту точку.
Пошаговый алгоритм построения касательной к окружности в заданной точке A:
- Для начала начертите произвольную окружность на листе бумаги. Обозначьте её центр точкой O.
- На окружности выберите и отметьте произвольную точку A — это будет точка касания касательной.
- Проведите прямую линию от центра окружности O к точке A. Эта линия называется радиусом окружности OA.
- Далее нужно построить прямую, проходящую через точку A, которая будет перпендикулярна радиусу OA.
- Для этого можно использовать угольник или транспортир, чтобы точно поставить прямой угол к радиусу OA в точке A.
- Проведите линию, перпендикулярную радиусу OA и проходящую через точку A. Эта линия и будет касательной к окружности в точке A.
Почему именно так?
В геометрии известно, что касательная к окружности в точке касания перпендикулярна радиусу, проведённому в эту точку. Это значит, что касательная линия никогда не пересекает окружность, кроме одной точки касания, и образует прямой угол с радиусом.
Поэтому построение перпендикуляра к радиусу в точке касания гарантирует, что построенная прямая будет касательной к окружности именно в этой точке.
Итог: после выполнения этих шагов вы получите касательную линию, которая касается окружности только в одной точке A и перпендикулярна радиусу OA.
