Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 408 Дорофеев, Шарыгин — Подробные Ответы
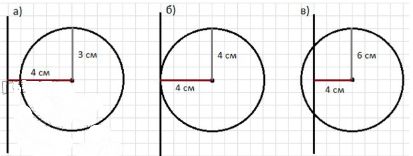
Что можно сказать о взаимном расположении прямой и окружности, если расстояние от центра окружности до прямой равно 4 см, а радиус окружности равен: а) Зсм; б) 4 см; в) б см?
Подсказка. Сделайте схематический рисунок.
Дано:
- Расстояние от центра окружности до прямой равно 4 см.
- Радиус окружности:
- а) 3 см
- б) 4 см
- в) 6 см
Рассмотрим взаимное расположение прямой и окружности в каждом случае:
а) Радиус окружности 3 см (меньше расстояния до прямой):
Прямая находится на расстоянии больше радиуса от центра окружности, значит прямая не пересекает окружность и не касается её.
Вывод: прямая и окружность не пересекаются.
б) Радиус окружности 4 см (равен расстоянию до прямой):
Расстояние от центра до прямой равно радиусу, значит прямая касается окружности в одной точке (касательная).
Вывод: прямая касается окружности.
в) Радиус окружности 6 см (больше расстояния до прямой):
Прямая находится ближе к центру, чем радиус, значит прямая пересекает окружность в двух точках.
Вывод: прямая пересекает окружность в двух точках.
Дано:
- Расстояние от центра окружности до прямой равно 4 сантиметрам.
- Радиус окружности задан в трех вариантах:
- а) 3 см;
- б) 4 см;
- в) 6 см.
Рассмотрим взаимное расположение прямой и окружности в каждом случае, используя геометрическую интерпретацию.
а) Радиус окружности 3 см (меньше расстояния от центра до прямой):
Поскольку радиус меньше расстояния от центра до прямой, это значит, что прямая расположена дальше от центра, чем достигает окружность. Таким образом, прямая не пересекает окружность и не касается её.
На схематическом рисунке это будет выглядеть как окружность, вокруг которой проходит прямая на расстоянии 4 см от центра, а радиус окружности всего 3 см, поэтому прямая находится снаружи окружности, не касаясь её.
Вывод: прямая и окружность не имеют общих точек — они не пересекаются.
б) Радиус окружности 4 см (равен расстоянию от центра до прямой):
Если радиус окружности равен расстоянию от центра до прямой, прямая касается окружности ровно в одной точке — это касательная прямая.
На схеме прямая касается окружности, «касается» её, как если бы окружность была опирается на прямую ровно в одной точке, расстояние от центра до прямой совпадает с радиусом.
Вывод: прямая является касательной к окружности.
в) Радиус окружности 6 см (больше расстояния от центра до прямой):
Когда радиус окружности больше расстояния от центра до прямой, значит прямая проходит через область окружности и пересекает её.
Геометрически это означает, что прямая проходит через окружность и имеет две точки пересечения с ней.
На рисунке это изображается как прямая, проходящая через окружность, пересекающая её в двух местах.
Вывод: прямая пересекает окружность в двух точках.
Обобщение:
Взаимное расположение прямой и окружности определяется сравнением расстояния от центра окружности до прямой и радиуса окружности:
- Если расстояние больше радиуса — прямой и окружность не пересекаются.
- Если расстояние равно радиусу — прямая касательная.
- Если расстояние меньше радиуса — прямая пересекает окружность в двух точках.
