
Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 404 Дорофеев, Шарыгин — Подробные Ответы
Расположите в порядке убывания дроби \(\frac{5}{11}, \frac{3}{7}, 0,5\).
Рассчитаем десятичные значения дробей:
\(\frac{5}{11} \approx 0,4545\),
\(\frac{3}{7} \approx 0,428571\),
\(0,5 = 0,5\).
Сравним значения:
\(0,5 > 0,4545 > 0,428571\).
В порядке убывания:
\(0,5 > \frac{5}{11} > \frac{3}{7}\).
Для того чтобы расположить дроби \(\frac{5}{11}\), \(\frac{3}{7}\) и число \(0,5\) в порядке убывания, необходимо сначала привести их к единому виду для удобства сравнения. Поскольку дроби и десятичные числа имеют разное представление, проще всего перевести дроби в десятичный формат. Это позволяет сравнивать числа напрямую по их десятичным значениям.
Вычислим десятичные значения дробей. Для \(\frac{5}{11}\) делим 5 на 11, что даёт приблизительно \(0,4545\), так как 11 умещается в 5 около 0,4545 раза с периодом. Для дроби \(\frac{3}{7}\) делим 3 на 7, получая примерно \(0,428571\), это бесконечная периодическая десятичная дробь. Число \(0,5\) уже представлено в десятичном виде и равно \(0,5\). Теперь у нас есть три числа в десятичной форме: \(0,4545\), \(0,428571\) и \(0,5\).
Сравним эти значения между собой. Число \(0,5\) больше, чем \(0,4545\), так как \(0,5 > 0,4545\). В свою очередь, \(0,4545\) больше, чем \(0,428571\), то есть \(0,4545 > 0,428571\). Значит, в порядке убывания наши числа расположатся так: \(0,5 > \frac{5}{11} > \frac{3}{7}\). Таким образом, исходные дроби и число упорядочены по убыванию значений.


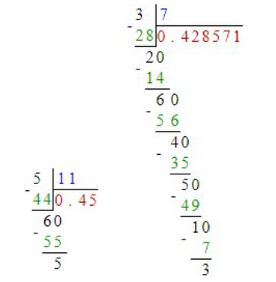


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!