Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 397 Дорофеев, Шарыгин — Подробные Ответы
а) Моторная лодка плыла 2,5 ч по течению реки, а потом 2 ч по озеру. Собственная скорость лодки 32 км/ч, а скорость течения реки 2,4 км/ч. Какое расстояние проплыла за это время моторная лодка?
б) Туристы плыли 4,5 ч на плоту, а затем 1,5 ч на байдарке. Скорость течения реки 2 км/ч, а скорость байдарки в стоячей воде 20 км/ч. Какое расстояние проплыли туристы?
а)
1) Скорость лодки по течению реки:
32 + 2,4 = 34,4 км/ч
2) Лодка проплыла расстояние:
2,5 × 34,4 + 2 × 32 = 86 + 64 = 150 км
Ответ: 150 км.
б)
1) Скорость байдарки по течению реки:
20 + 2 = 22 км/ч
2) Туристы проплыли расстояние:
4,5 × 2 + 1,5 × 22 = 9 + 33 = 42 км
Ответ: 42 км.
а)
1) Определим скорость моторной лодки по течению реки. Поскольку лодка движется по течению, её скорость равна сумме собственной скорости и скорости течения:
Собственная скорость лодки 32 км/ч
Скорость течения реки 2,4 км/ч
Скорость лодки по течению равна 32 + 2,4 = 34,4 км/ч
2) Рассчитаем расстояние, которое лодка проплыла за 2,5 часа по течению:
Время движения 2,5 часа
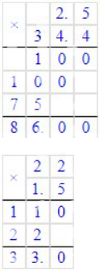
Расстояние равно 34,4 × 2,5 = 86 км
3) Теперь определим расстояние, которое лодка проплыла за 2 часа по озеру, где течение отсутствует. Скорость лодки в озере равна собственной скорости:
Время движения 2 часа
Расстояние равно 32 × 2 = 64 км
4) Найдём общее расстояние, пройденное лодкой, сложив оба расстояния:
Общее расстояние равно 86 + 64 = 150 км
Ответ: моторная лодка проплыла 150 км.
б)
1) Определим скорость туристов на плоту. Поскольку плот движется вместе с течением, его скорость равна скорости течения реки:
Скорость течения реки 2 км/ч
Скорость плота равна 2 км/ч
2) Рассчитаем расстояние, пройденное туристами на плоту за 4,5 часа:
Время движения 4,5 часа
Расстояние равно 2 × 4,5 = 9 км
3) Теперь определим скорость байдарки по течению. Скорость байдарки равна сумме собственной скорости и скорости течения:
Собственная скорость байдарки 20 км/ч
Скорость течения реки 2 км/ч
Скорость байдарки по течению равна 20 + 2 = 22 км/ч
4) Рассчитаем расстояние, пройденное туристами на байдарке за 1,5 часа:
Время движения 1,5 часа
Расстояние равно 22 × 1,5 = 33 км
5) Найдём общее расстояние, пройденное туристами, сложив расстояния на плоту и байдарке:
Общее расстояние равно 9 + 33 = 42 км
Ответ: туристы проплыли 42 км.
