Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 389 Дорофеев, Шарыгин — Подробные Ответы
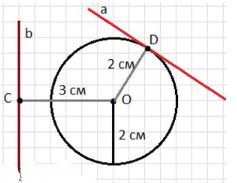
Начертите окружность и две прямые, одна из которых пересекает окружность, а другая нет. Измерьте расстояние от центра окружности до каждой из этих прямых. Введите обозначения и запишите ответ.
Дано:
- Расстояние от точки O до прямой a равно AD = 2 см;
- Расстояние от точки O до прямой b равно OC = 3 см.
Это означает, что перпендикуляр, опущенный из точки O на прямую a, имеет длину 2 см, а на прямую b — длину 3 см.
Обозначим расстояния от точки до прямых как:
- dₐ = AD = 2 см;
- d_b = OC = 3 см.
Таким образом, расстояния от точки O до прямых a и b равны 2 см и 3 см соответственно.
Дано условие задачи:
- Расстояние от точки O до прямой a обозначено как AD и равно 2 см;
- Расстояние от точки O до прямой b обозначено как OC и равно 3 см.
Объясним, что означает данное условие. Расстояние от точки до прямой — это длина перпендикуляра, опущенного из этой точки на прямую. Таким образом, из точки O опущен перпендикуляр на прямую a, и длина этого перпендикуляра равна 2 сантиметрам.
Аналогично, из точки O опущен перпендикуляр на прямую b, длина которого составляет 3 сантиметра.
Для удобства обозначим эти расстояния как:
- Расстояние до прямой a — dₐ = AD = 2 см;
- Расстояние до прямой b — d_b = OC = 3 см.
Эти значения важны при решении задач, связанных с расположением точек и прямых на плоскости, а также при вычислении расстояний и углов между элементами геометрических фигур.
Итог: расстояния от точки O до прямых a и b равны 2 см и 3 см соответственно.
