
Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 380 Дорофеев, Шарыгин — Подробные Ответы
Выразите приближённо обыкновенную дробь десятичной дробью с одним, двумя, тремя знаками после запятой:
а) \(\frac{2}{3}\);
б) \(\frac{5}{6}\);
в) \(\frac{2}{9}\);
г) \(\frac{4}{7}\).
а) Чтобы выразить \(\frac{2}{3}\) десятичной дробью, делим 2 на 3, получаем \(0{,}6666\ldots\). Округляем с разной точностью: с тремя знаками после запятой \(0{,}667\), двумя \(0{,}67\), одним \(0{,}7\).
б) Делим 5 на 6, получаем \(0{,}83333\ldots\). Округляем: \(0{,}833\), \(0{,}83\), \(0{,}8\).
в) Делим 2 на 9, получаем \(0{,}22222\ldots\). Округляем: \(0{,}222\), \(0{,}22\), \(0{,}2\).
г) Делим 4 на 7, получаем \(0{,}57142857\ldots\). Округляем: \(0{,}571\), \(0{,}57\), \(0{,}6\).
а) Чтобы перевести обыкновенную дробь \(\frac{2}{3}\) в десятичную, нужно выполнить деление числителя на знаменатель. Делим 2 на 3 и получаем периодическую десятичную дробь \(0{,}6666\ldots\), где цифра 6 повторяется бесконечно. Для практического использования часто требуется округлить число до определённого количества знаков после запятой. Например, округляя до трёх знаков, получаем \(0{,}667\), что означает приближение с точностью до тысячных. Если округлить до двух знаков, результат будет \(0{,}67\), а при округлении до одного знака — \(0{,}7\). Каждое последующее сокращение знаков после запятой уменьшает точность, но упрощает запись числа.
б) Аналогично для дроби \(\frac{5}{6}\) делим 5 на 6. В результате получается периодическая десятичная дробь \(0{,}83333\ldots\), где цифра 3 повторяется бесконечно. Округляя до трёх знаков после запятой, получаем \(0{,}833\), что достаточно точно отражает значение дроби. При округлении до двух знаков после запятой результат будет \(0{,}83\), а до одного знака — \(0{,}8\). Такое округление удобно для быстрого приближённого вычисления, когда точность до тысячных не требуется.
в) Для дроби \(\frac{2}{9}\) деление 2 на 9 даёт периодическую десятичную дробь \(0{,}22222\ldots\), где цифра 2 повторяется бесконечно. Округление до трёх знаков после запятой даёт \(0{,}222\), что уже является хорошим приближением. При сокращении знаков после запятой до двух и одного получаем \(0{,}22\) и \(0{,}2\) соответственно. Такое приближение удобно для повседневных расчетов, где не требуется высокая точность.
г) Для дроби \(\frac{4}{7}\) результат деления 4 на 7 — периодическая десятичная дробь \(0{,}57142857\ldots\), где последовательность цифр повторяется. При округлении до трёх знаков после запятой получаем \(0{,}571\), что даёт точное приближение. Если округлить до двух знаков, результат будет \(0{,}57\), а при округлении до одного знака — \(0{,}6\). Чем меньше знаков после запятой, тем меньше точность, но проще запись и быстрее вычисления.


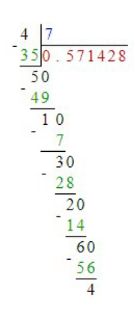
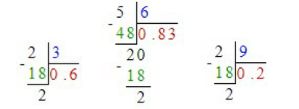


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!