
Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 379 Дорофеев, Шарыгин — Подробные Ответы
Даны дроби: \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}, \frac{1}{7}, \frac{1}{8}, \frac{1}{9}, \frac{1}{10}, \frac{1}{11}, \frac{1}{12}\).
Какие из них можно представить в виде десятичных дробей? Если дробь нельзя представить в виде десятичной дроби, то запишите её приближённое значение с двумя знаками после запятой.
В виде десятичных дробей можно представить дроби:
\(\frac{1}{2} = 0,5\),
\(\frac{1}{4} = 0,25\),
\(\frac{1}{5} = 0,2\),
\(\frac{1}{8} = 0,125\),
\(\frac{1}{10} = 0,1\).
Это возможно, так как знаменатели этих дробей разлагаются на степени двойки и пятёрки.
Нельзя представить в виде десятичных дробей:
\(\frac{1}{3} = 0,3333 \ldots \approx 0,33\),
\(\frac{1}{6} = 0,16666 \ldots \approx 0,17\),
\(\frac{1}{7} = 0,142857142 \ldots \approx 0,14\),
\(\frac{1}{9} = 0,1111 \ldots \approx 0,11\),
\(\frac{1}{11} = 0,090909 \ldots \approx 0,09\),
\(\frac{1}{12} = 0,08333 \ldots \approx 0,08\).
Эти дроби имеют знаменатели с простыми делителями, отличными от 2 и 5, поэтому их десятичные представления бесконечны и периодичны.
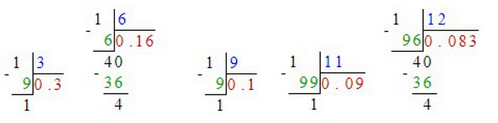
В десятичной записи дроби можно представить точно только тогда, когда в её знаменателе после сокращения остаются простые делители 2 и 5, так как десятичная система основана на числе 10 = \(2^1 \cdot 5^1\). Если знаменатель дроби можно представить в виде \(2^m \cdot 5^n\), где \(m\) и \(n\) — неотрицательные целые числа, тогда дробь будет иметь конечное количество знаков после запятой. Например, дроби \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{5}\), \(\frac{1}{8}\), \(\frac{1}{10}\) удовлетворяют этому условию, поэтому их десятичные представления конечны и равны соответственно \(0,5\), \(0,25\), \(0,2\), \(0,125\), \(0,1\).
Если же знаменатель содержит другие простые делители, отличные от 2 и 5, десятичное представление дроби будет бесконечным периодическим. Например, дробь \(\frac{1}{3}\) имеет знаменатель 3, который не делится на 2 или 5, поэтому её десятичное представление — бесконечная периодическая дробь \(0,3333 \ldots\). Аналогично, дроби \(\frac{1}{6}\), \(\frac{1}{7}\), \(\frac{1}{9}\), \(\frac{1}{11}\), \(\frac{1}{12}\) имеют в знаменателях простые делители, отличные от 2 и 5, что приводит к бесконечным периодическим десятичным дробям. Их значения можно лишь приблизительно записать с ограниченным количеством знаков после запятой: \(\frac{1}{3} \approx 0,33\), \(\frac{1}{6} \approx 0,17\), \(\frac{1}{7} \approx 0,14\), \(\frac{1}{9} \approx 0,11\), \(\frac{1}{11} \approx 0,09\), \(\frac{1}{12} \approx 0,08\).
Таким образом, основное правило для определения, можно ли представить дробь в виде конечной десятичной дроби, сводится к анализу её знаменателя. Если знаменатель сводится к произведению степеней двойки и пятёрки, дробь будет иметь конечное десятичное представление. Во всех остальных случаях десятичное выражение будет бесконечным и периодическим, что требует округления для практического использования. Это объясняет, почему дроби с знаменателями 2, 4, 5, 8 и 10 имеют точные десятичные эквиваленты, а дроби с знаменателями 3, 6, 7, 9, 11, 12 — только приближённые значения.


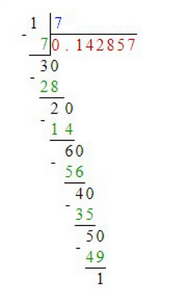


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!