ГДЗ по Математике 6 Класс Номер 320 Дорофеев, Шарыгин — Подробные Ответы

Действуем по алгоритму.
Выполните следующее построение:
• проведите две пересекающиеся прямые;
• начертите окружность с центром в точке пересечения прямых;
• обозначьте точки пересечения прямых и окружности;
• соедините отрезками каждую пару соседних точек.
Как надо было провести пару прямых, чтобы получился:
а) квадрат;
б) прямоугольник произвольного вида?

1) Для построения, согласно алгоритму, сначала проведём две пересекающиеся прямые. Они должны пересекаться под определённым углом в одной точке.

2) Затем вокруг точки пересечения проведём окружность с центром в этой точке. Окружность пересечёт каждую прямую в двух точках.

3) Обозначим эти точки пересечения – всего будет четыре точки (по две на каждой прямой).

4) Соедините отрезками каждую пару соседних точек, чтобы получить четырехугольник.

Ответы на вопросы:

а) Чтобы получился квадрат, нужно провести прямые так, чтобы они пересекались под углом 90 градусов (перпендикулярно). Тогда все стороны полученного четырехугольника будут равны, а углы — прямыми, что и определяет квадрат.

б) Чтобы получился прямоугольник произвольного вида, прямые также должны быть перпендикулярны, но при этом длины отрезков между точками пересечения окружности и прямых могут отличаться. Таким образом, стороны будут попарно равны, а углы — прямыми, что соответствует прямоугольнику, не обязательно квадрату.

1) Выполним построение по заданному алгоритму. Сначала проведём две прямые линии так, чтобы они пересекались в одной точке. Эти две прямые пересекаются, образуя четыре угла. Точка их пересечения станет центром нашей окружности.

2) Далее вокруг этой точки пересечения проведём окружность с центром в ней. Окружность пересечёт каждую из двух прямых в двух точках, всего на окружности будет четыре точки пересечения — по две на каждой прямой.

3) Обозначим все четыре точки пересечения прямых с окружностью. Эти точки расположены на окружности и на прямых, исходящих из центра окружности.

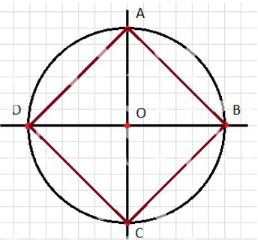
4) Соединим отрезками каждую пару соседних точек на окружности, получив таким образом четырёхугольник, вписанный в окружность с вершинами в точках пересечения прямых и окружности.

Ответ на вопросы:

а) Чтобы получился квадрат, необходимо провести две прямые так, чтобы они пересекались под прямым углом — 90 градусов. Перпендикулярность прямых гарантирует, что углы четырёхугольника будут прямыми. Благодаря тому, что вершины лежат на окружности, и углы равны 90 градусам, стороны будут равны, что соответствует свойствам квадрата.

б) Чтобы получить прямоугольник произвольного вида, также нужно провести две прямые, пересекающиеся под прямым углом 90 градусов. Однако длины отрезков между точками пересечения окружности и прямых могут отличаться, в отличие от квадрата. Это приведёт к тому, что стороны четырёхугольника будут попарно равны, а углы — прямыми, но стороны не будут одинаковыми, что и соответствует свойствам прямоугольника, не являющегося квадратом.

Таким образом, ключевым условием для обоих фигур является перпендикулярное пересечение прямых, а разницей между квадратом и прямоугольником является равенство всех сторон в первом случае и равенство только противоположных сторон во втором.