Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 290 Дорофеев, Шарыгин — Подробные Ответы
Действуем по правилу.
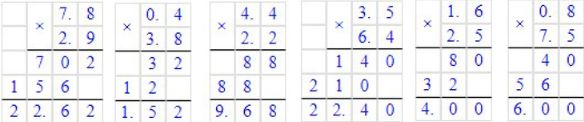
Выполните умножение:
а) 7,8 * 2,9;
б) 0,4 * 3,8;
в) 4,4 * 2,2;
г) 3,5 * 6,4;
д) 1,6 * 2,5;
е) 0,8 * 7,5.
Задача: Выполните умножение десятичных дробей:
а) 7,8 × 2,9
Перемножим числа без запятой: 78 × 29 = 2262
В исходных числах после запятой всего 2 знака (7,8 — 1 знак, 2,9 — 1 знак).
Перемещаем запятую в результате на 2 знака слева направо: 22,62
Ответ: 22,62
б) 0,4 × 3,8
Перемножим без запятой: 4 × 38 = 152
В исходных числах 1 + 1 = 2 знака после запятой.
Перемещаем запятую на 2 знака: 1,52
Ответ: 1,52
в) 4,4 × 2,2
Перемножим без запятой: 44 × 22 = 968
В исходных числах 1 + 1 = 2 знака после запятой.
Перемещаем запятую на 2 знака: 9,68
Ответ: 9,68
г) 3,5 × 6,4
Перемножим без запятой: 35 × 64 = 2240
В исходных числах 1 + 1 = 2 знака после запятой.
Перемещаем запятую на 2 знака: 22,40 или 22,4
Ответ: 22,4
д) 1,6 × 2,5
Перемножим без запятой: 16 × 25 = 400
В исходных числах 1 + 1 = 2 знака после запятой.
Перемещаем запятую на 2 знака: 4,00 или 4
Ответ: 4
е) 0,8 × 7,5
Перемножим без запятой: 8 × 75 = 600
В исходных числах 1 + 1 = 2 знака после запятой.
Перемещаем запятую на 2 знака: 6,00 или 6
Ответ: 6
Задача: Выполните умножение десятичных дробей, следуя правилу умножения:
Чтобы умножить десятичные дроби, следует:
- Перемножить числа, игнорируя запятые;
- Подсчитать общее количество знаков после запятой в обоих множителях;
- В полученном результате сдвинуть запятую влево на это количество знаков.
а) 7,8 × 2,9
Перемножим без запятой: 78 × 29 = 2262.
В первом числе после запятой 1 знак, во втором — 1 знак, всего 2 знака.
Перемещаем запятую в произведении на 2 знака влево:
2262 → 22,62.
Ответ: 22,62.
б) 0,4 × 3,8
Перемножим без запятой: 4 × 38 = 152.
Количество знаков после запятой: 1 + 1 = 2.
Перемещаем запятую на 2 знака влево:
152 → 1,52.
Ответ: 1,52.
в) 4,4 × 2,2
Перемножим без запятой: 44 × 22 = 968.
Количество знаков после запятой: 1 + 1 = 2.
Перемещаем запятую на 2 знака влево:
968 → 9,68.
Ответ: 9,68.
г) 3,5 × 6,4
Перемножим без запятой: 35 × 64 = 2240.
Количество знаков после запятой: 1 + 1 = 2.
Перемещаем запятую на 2 знака влево:
2240 → 22,40 или 22,4.
Ответ: 22,4.
д) 1,6 × 2,5
Перемножим без запятой: 16 × 25 = 400.
Количество знаков после запятой: 1 + 1 = 2.
Перемещаем запятую на 2 знака влево:
400 → 4,00 или 4.
Ответ: 4.
е) 0,8 × 7,5
Перемножим без запятой: 8 × 75 = 600.
Количество знаков после запятой: 1 + 1 = 2.
Перемещаем запятую на 2 знака влево:
600 → 6,00 или 6.
Ответ: 6.
Итог: при умножении десятичных дробей всегда удобно сначала умножить числа без запятой, а затем правильно поставить запятую в результате, учитывая количество десятичных знаков в исходных множителях.
