Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 248 Дорофеев, Шарыгин — Подробные Ответы
Действуем по правилу.
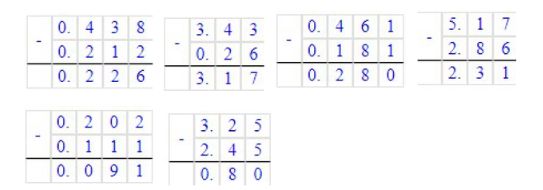
Выполните вычитание:
а) 0,438 — 0,212;
б) 3,43 — 0,26;
в) 0,461 — 0,181;
г) 5,17 — 2,86;
д) 0,202 — 0,111;
е) 3,25 — 2,45.
Вычитание десятичных дробей с подробными объяснениями
а) 0,438 − 0,212
Вычитаем по разрядам справа налево:
- Тысячные: 8 − 2 = 6;
- Сотые: 3 − 1 = 2;
- Десятые: 4 − 2 = 2.
Результат: 0,226.
б) 3,43 − 0,26
Приведём к сотым и вычитаем:
- Сотые: 3 − 6 — нужно взять в долг;
3,43 = 3,430
Вычитание:
- Сотые: 30 − 6 = 24;
- Десятые: 3 − 2 − 1 (заём) = 0;
- Целые: 3 − 0 = 3.
Результат: 3,17.
в) 0,461 − 0,181
- Тысячные: 1 − 1 = 0;
- Сотые: 6 − 8 — нужен заём;
Берём в долг из десятых: 6 + 10 = 16;
- Сотые: 16 − 8 = 8;
- Десятые: 4 − 1 − 1 (заём) = 2;
- Целые: 0 − 0 = 0.
Результат: 0,280.
г) 5,17 − 2,86
- Сотые: 7 − 6 = 1;
- Десятые: 1 − 8 — нужен заём;
Берём в долг из целых: 5 − 1 = 4, десятые: 1 + 10 = 11;
- Десятые: 11 − 8 = 3;
- Целые: 4 − 2 = 2.
Результат: 2,31.
д) 0,202 − 0,111
- Тысячные: 2 − 1 = 1;
- Сотые: 0 − 1 — нужен заём;
Берём в долг из десятых: 0 + 10 = 10;
- Сотые: 10 − 1 = 9;
- Десятые: 2 − 1 − 1 (заём) = 0;
- Целые: 0 − 0 = 0.
Результат: 0,091.
е) 3,25 − 2,45
- Сотые: 5 − 5 = 0;
- Десятые: 2 − 4 — нужен заём;
Берём в долг из целых: 3 − 1 = 2, десятые: 2 + 10 = 12;
- Десятые: 12 − 4 = 8;
- Целые: 2 − 2 = 0.
Результат: 0,80.
Общий вывод:
Вычитание десятичных дробей требует точного выравнивания чисел по десятичной точке и поразрядного вычитания справа налево с учётом займов. Такой метод гарантирует правильность и точность вычислений.
Подробное поэтапное выполнение вычитания десятичных дробей
а) Вычисление 0,438 − 0,212
Для начала выровняем числа по десятичной точке:
0,438
−0,212
Выполним вычитание по разрядам:
- Тысячные: 8 − 2 = 6;
- Сотые: 3 − 1 = 2;
- Десятые: 4 − 2 = 2.
Итоговый результат: 0,226.
б) Вычисление 3,43 − 0,26
Запишем с учётом сотых:
3,43
−0,26
Выполним вычитание:
- Сотые: 3 − 6 — не можем, займём 1 у десятых;
- Десятые: (4 − 1) − 2 = 1;
- Сотые: (3 + 10) − 6 = 7;
- Целая часть: 3 − 0 = 3.
Итог: 3,17.
в) Вычисление 0,461 − 0,181
Выполним вычитание по разрядам:
- Тысячные: 1 − 1 = 0;
- Сотые: 6 − 8 — займём 1 у десятых;
- Десятые: (4 − 1) − 1 = 2;
- Сотые: (6 + 10) − 8 = 8;
- Целая часть: 0 − 0 = 0.
Итог: 0,280.
г) Вычисление 5,17 − 2,86
Вычитаем по разрядам:
- Сотые: 7 − 6 = 1;
- Десятые: 1 − 8 — займём 1 у целых;
- Десятые: (1 + 10) − 8 = 3;
- Целая часть: (5 − 1) − 2 = 2.
Итог: 2,31.
д) Вычисление 0,202 − 0,111
Вычитаем разряды:
- Тысячные: 2 − 1 = 1;
- Сотые: 0 − 1 — займём 1 у десятых;
- Десятые: (2 − 1) − 1 = 0;
- Сотые: (0 + 10) − 1 = 9;
- Целая часть: 0 − 0 = 0.
Итог: 0,091.
е) Вычисление 3,25 − 2,45
Вычитаем по разрядам:
- Сотые: 5 − 5 = 0;
- Десятые: 2 − 4 — займём 1 у целых;
- Десятые: (2 + 10) − 4 = 8;
- Целая часть: (3 − 1) − 2 = 0.
Итог: 0,80.
Общий вывод:
Для корректного вычитания десятичных дробей необходимо правильно выровнять их по десятичной точке и выполнять вычитание по разрядам, начиная с самых маленьких (справа налево). При недостатке цифры в разряде следует брать «заём» у следующего разряда слева, что позволяет получить правильный результат. Такой метод обеспечивает точность и правильность вычислений с десятичными дробями.
