Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 244 Дорофеев, Шарыгин — Подробные Ответы
Постройте прямые a и b, пересекающиеся под углом 50 градусов. Проведите какую-нибудь прямую, параллельную прямой а, и прямую, параллельную прямой b. Определите, чему равны величины углов четырёхугольника, вершинами которого являются точки пересечения прямых.
Построение и анализ четырёхугольника, образованного прямыми
1. Построение прямых a и b, пересекающихся под углом 50°
Начнем с двух прямых, которые пересекаются в точке O под углом 50°. Это означает, что угол между ними равен 50°, а дополнительный угол при пересечении равен 130° (так как сумма смежных углов равна 180°).
2. Проведение прямых, параллельных a и b
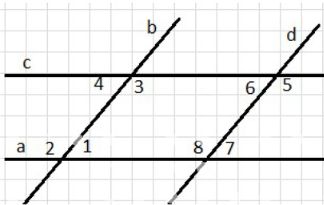
Проведем прямую c, параллельную прямой a, и прямую d, параллельную прямой b.
В результате пересечения прямой c с прямой d и прямой b с прямой c образуется четырёхугольник, вершинами которого являются точки пересечения этих прямых.
3. Определение величин углов четырёхугольника
Четырёхугольник, образованный двумя параллельными прямыми и двумя другими пересекающимися прямыми, является параллелограммом.
В параллелограмме противоположные углы равны, а сумма соседних углов равна 180°.
Исходя из угла пересечения a и b (50°), углы при пересечении с параллельными прямыми сохраняют свои величины из-за свойств параллельных и секущих прямых:
- Два угла равны 50°;
- Два угла равны 130°.
Таким образом, углы четырёхугольника равны по парам:
50°, 130°, 50°, 130°.
4. Итог
Построив две прямые a и b, пересекающиеся под углом 50°, и две прямые, параллельные им, образуется параллелограмм с углами 50° и 130°, расположенными попарно.
Заключение:
Свойства параллельных прямых и углы, образованные секущими, позволяют определить величины углов в образованном четырёхугольнике, что является важным элементом геометрических построений и доказательств.
Подробное построение и анализ четырёхугольника, образованного пересечением прямых
1. Построение прямых a и b, пересекающихся под углом 50°
Начинаем с построения двух прямых — a и b — которые пересекаются в точке O под углом 50°. Это означает, что угол между ними составляет 50°. При пересечении прямых образуются также смежные углы, которые дополняют 50° до 180°, то есть равны 130°.
Иллюстративно:
- Угол между a и b: 50°;
- Смежный угол: 130°.
2. Проведение прямых, параллельных a и b
Далее проведём прямую c, параллельную прямой a, и прямую d, параллельную прямой b. Согласно свойствам параллельных прямых, углы, образуемые пересечением с секущими, сохраняют величины, равные углам между исходными прямыми.
В результате пересечений прямых b и c, а также a и d, образуется четырёхугольник, вершинами которого являются точки пересечения этих прямых.
3. Определение величин углов четырёхугольника
Четырёхугольник, образованный двумя параллельными прямыми и двумя другими пересекающимися прямыми, является параллелограммом. В параллелограмме:
- Противоположные углы равны;
- Сумма соседних углов равна 180°.
Исходя из угла 50° между прямыми a и b, углы четырёхугольника распределяются следующим образом:
- Два угла равны 50°;
- Два угла равны 130°.
4. Расчёт и доказательство
Пусть точки пересечения прямых обозначены как A, B, C и D.
Угол при вершине A равен 50°, так как это угол между a и b.
Угол при вершине B — 130°, смежный с 50°.
Углы при вершинах C и D соответствуют углам при A и B соответственно, поскольку прямые c и d параллельны a и b.
Таким образом, углы четырёхугольника составляют 50°, 130°, 50°, 130°.
5. Итог
Построив две прямые, пересекающиеся под углом 50°, и две прямые, параллельные им, мы получаем четырёхугольник — параллелограмм с парами углов 50° и 130°.
Заключение:
Данная задача демонстрирует важные свойства параллельных и пересекающихся прямых в планиметрии, а также помогает понять, как углы при пересечении и параллельности формируют углы многоугольников. Эти знания применимы в геометрических построениях, решениях задач и доказательствах.
