Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 214 Дорофеев, Шарыгин — Подробные Ответы
Рассуждаем.
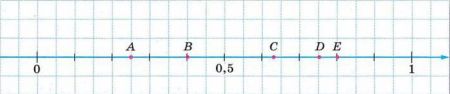
Для каждого из чисел \( \frac{2}{5} \), \( \frac{4}{5} \), \( \frac{1}{4} \), \( \frac{3}{4} \), \( \frac{5}{8} \) укажите соответствующую ему точку (рис. 3.8).
\( \frac{2}{5} = \frac{4}{10} = 0{,}4 \);
\( \frac{4}{5} = \frac{8}{10} = 0{,}8 \);
\( \frac{1}{4} = \frac{25}{100} = 0{,}25 \);
\( \frac{3}{4} = \frac{75}{100} = 0{,}75 \);
\( \frac{5}{8} = \frac{625}{1000} = 0{,}625 \).
Теперь упорядочим десятичные дроби по возрастанию:
0,25 < 0,4 < 0,625 < 0,75 < 0,8.
Соответственно, и сами дроби сравниваются так:
\( \frac{1}{4} < \frac{2}{5} < \frac{5}{8} < \frac{3}{4} < \frac{4}{5} \).
Обозначим дроби буквами:
A = \( \frac{1}{4} \);
B = \( \frac{2}{5} \);
C = \( \frac{5}{8} \);
D = \( \frac{3}{4} \);
E = \( \frac{4}{5} \).
Их порядок по возрастанию:
A (\( \frac{1}{4} \)) < B (\( \frac{2}{5} \)) < C (\( \frac{5}{8} \)) < D (\( \frac{3}{4} \)) < E (\( \frac{4}{5} \)).
\( \frac{2}{5} \) — приводим к знаменателю 10, умножив числитель и знаменатель на 2: \( \frac{2}{5} = \frac{4}{10} \). В десятичной форме это 0,4.
\( \frac{4}{5} \) — приводим к знаменателю 10, умножая на 2: \( \frac{4}{5} = \frac{8}{10} = 0{,}8 \).
\( \frac{1}{4} \) — приводим к знаменателю 100, умножая на 25: \( \frac{1}{4} = \frac{25}{100} = 0{,}25 \).
\( \frac{3}{4} \) — приводим к знаменателю 100, умножая на 25: \( \frac{3}{4} = \frac{75}{100} = 0{,}75 \).
\( \frac{5}{8} \) — приводим к знаменателю 1000, умножая на 125: \( \frac{5}{8} = \frac{625}{1000} = 0{,}625 \).
Теперь, когда дроби представлены десятичными числами, их легче сравнивать.
Сравним десятичные дроби в порядке возрастания:
0,25 (\( \frac{1}{4} \)) < 0,4 (\( \frac{2}{5} \)) < 0,625 (\( \frac{5}{8} \)) < 0,75 (\( \frac{3}{4} \)) < 0,8 (\( \frac{4}{5} \)).
Это значит, что исходные дроби расположены по возрастанию именно в таком порядке:
\( \frac{1}{4} < \frac{2}{5} < \frac{5}{8} < \frac{3}{4} < \frac{4}{5} \).
Обозначим дроби буквами для удобства:
A — \( \frac{1}{4} \);
B — \( \frac{2}{5} \);
C — \( \frac{5}{8} \);
D — \( \frac{3}{4} \);
E — \( \frac{4}{5} \).
Итоговый порядок этих дробей:
A < B < C < D < E
