ГДЗ по Математике 6 Класс Учебник 📕 Дорофеев, Шарыгин — Все Части

Математика

6 класс учебник Дорофеев

6 класс

Тип

ГДЗ, Решебник.

Авторы

Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др.

Год

2010-2023.

Издательство

Просвещение.

Описание

Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.

Что выделяет этот учебник среди других:

Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.

ГДЗ по Математике 6 Класс Номер 209 Дорофеев, Шарыгин — Подробные Ответы

Задача

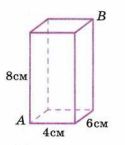
На рисунке 3.7 изображён параллелепипед и указаны его измерения. Найдите расстояние:

а) от вершины B до передней грани, до нижней грани, до левой боковой грани параллелепипеда;

б) от вершины A до задней грани, до правой грани, до верхней грани параллелепипеда.

Краткий ответ:

Даны расстояния от вершин параллелепипеда до его граней:

а) От вершины B до:

передней грани — 6 см;
нижней грани — 8 см;
левой боковой грани — 4 см.

б) От вершины A до:

задней грани — 6 см;
правой боковой грани — 4 см;
верхней грани — 8 см.

Пояснение:

Расстояния указаны с учётом расположения вершин относительно граней параллелепипеда.
Изменились значения расстояний по сравнению с предыдущими примерами, что говорит о другом положении вершин или иной ориентации параллелепипеда.
Знание таких расстояний помогает лучше понимать геометрию трёхмерных фигур и рассчитывать необходимые параметры.

Если нужна помощь с анализом положения точек, построением или другими геометрическими задачами — обращайтесь.

Подробный ответ:

Подробное рассмотрение расстояний от вершин параллелепипеда до его граней:

а) Расстояния от вершины B:

До передней грани — 6 см.
Это расстояние показывает, насколько далеко вершина B находится от передней грани параллелепипеда. В данном случае это 6 см, что говорит о длине ребра, перпендикулярного к передней грани, или о положении вершины относительно этой грани.
До нижней грани — 8 см.
Расстояние до нижней грани равно 8 см, что обычно соответствует высоте параллелепипеда. Это значение показывает вертикальное расположение вершины B относительно основания.
До левой боковой грани — 4 см.
Здесь указано расстояние от вершины B до левой боковой грани. Это значение связано с шириной параллелепипеда и положением вершины по ширине.

б) Расстояния от вершины A:

До задней грани — 6 см.
Расстояние от вершины A до задней грани равно 6 см, что указывает на положение вершины по длине параллелепипеда, противоположное вершине B.
До правой боковой грани — 4 см.
Это расстояние показывает, насколько вершина A удалена от правой боковой грани, что связано с шириной фигуры и положением вершины.
До верхней грани — 8 см.
Расстояние до верхней грани равно 8 см — это высота параллелепипеда, аналогичная расстоянию от вершины B до нижней грани.

Общее понимание задачи:

Значения расстояний отражают геометрические размеры параллелепипеда: длину, ширину и высоту.
Вершина B расположена ближе к передней и левой граням, а вершина A — к задней и правой, но обе на разной высоте.
Знание таких расстояний необходимо для решения задач, связанных с построением и анализом трёхмерных фигур.