Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 196 Дорофеев, Шарыгин — Подробные Ответы
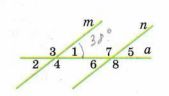
Прямые m и n параллельны, угол 1 = 38 градусов (рис. 3.6). Запишите величины всех углов, обозначенных цифрами.
∠1 = ∠2 = 38° — это вертикальные углы, они равны.
∠3 = 180° − ∠1 = 180° − 38° = 142° — это смежные углы, сумма которых равна 180°, значит, ∠3 равен 142°.
∠3 = ∠4 = 142° — вертикальные углы, они равны.
∠3 = ∠7 = 142° — так как прямые m и n параллельны и пересекаются прямой a, углы, образованные под одним углом, равны.
∠7 = ∠8 = 142° — вертикальные углы, они равны.
∠1 = ∠5 = 38° — углы, образованные параллельными прямыми m и n и пересечением прямой a под одним углом, равны.
∠5 = ∠6 = 38° — вертикальные углы, они равны.
Ответ:
∠1 = ∠2 = ∠5 = ∠6 = 38°;
∠3 = ∠4 = ∠7 = ∠8 = 142°.
Исходя из этих свойств, разберём данные углы:
∠1 и ∠2 равны, так как это вертикальные углы, и их величина — 38°.
∠3 — смежный угол к ∠1, поэтому его величина равна 180° − 38° = 142°.
∠3 и ∠4 — вертикальные углы, значит равны и равны 142°.
∠3 и ∠7 равны, потому что прямые m и n параллельны, а пересекающая их прямая a образует равные углы.
∠7 и ∠8 — вертикальные углы, следовательно, равны и равны 142°.
∠1 и ∠5 равны, так как прямые m и n параллельны и пересекаются прямой a под одним углом.
∠5 и ∠6 — вертикальные углы, поэтому равны и равны 38°.
Вывод:
Углы ∠1, ∠2, ∠5 и ∠6 равны между собой и равны 38°.
Углы ∠3, ∠4, ∠7 и ∠8 равны между собой и равны 142°.
