
Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 178 Дорофеев, Шарыгин — Подробные Ответы
а) \(\left(3-\frac{3}{7}\right) : \left(\frac{1}{14}+\frac{1}{4}\right) = \left(2\frac{7}{7}-\frac{3}{7}\right) : \frac{2+7}{28} = 2\frac{4}{7} : \frac{9}{28} = \frac{18}{7} : \frac{9}{28} = \frac{18}{7} \cdot \frac{28}{9} =\)
\(= \frac{18 \cdot 28}{7 \cdot 9} = \frac{2 \cdot 4}{1 \cdot 1} = 8.\)
б) \(\left(\frac{2}{9} + \frac{2}{15}\right) : \left(1\frac{1}{9} — \frac{2}{3}\right) = \frac{2 \cdot 5 + 2 \cdot 3}{45} : \frac{10}{9} — \frac{6}{9} = \frac{10 + 6}{45} : \frac{4}{9} = \frac{16}{45} \cdot \frac{9}{4} = \frac{16 \cdot 9}{45 \cdot 4} = \frac{4 \cdot 1}{5 \cdot 1} =\)
\(= \frac{4}{5}.\)
а) Рассмотрим выражение \(\left(3-\frac{3}{7}\right) : \left(\frac{1}{14}+\frac{1}{4}\right)\). Сначала упростим каждую часть отдельно. В числителе первой дроби \(3-\frac{3}{7}\) преобразуем число 3 к дроби с тем же знаменателем: \(3 = \frac{21}{7}\), тогда \(3-\frac{3}{7} = \frac{21}{7} — \frac{3}{7} = \frac{18}{7}\). Во второй части выражения складываем дроби \(\frac{1}{14}+\frac{1}{4}\). Для этого найдём общий знаменатель, который равен 28, и приведём дроби: \(\frac{1}{14} = \frac{2}{28}\), \(\frac{1}{4} = \frac{7}{28}\), следовательно сумма равна \(\frac{2}{28} + \frac{7}{28} = \frac{9}{28}\).
Теперь исходное выражение принимает вид \(\frac{18}{7} : \frac{9}{28}\). Деление дробей заменяем умножением на обратную дробь: \(\frac{18}{7} \cdot \frac{28}{9}\). Упрощаем числители и знаменатели: \(18\) и \(9\) делятся на 9, получаем \(2\) и \(1\) соответственно; \(28\) и \(7\) делятся на 7, получаем \(4\) и \(1\). В итоге остаётся \(2 \cdot 4 = 8\).
б) Рассмотрим выражение \(\left(\frac{2}{9} + \frac{2}{15}\right) : \left(1\frac{1}{9} — \frac{2}{3}\right)\). Сначала упростим сумму в скобках слева. Найдём общий знаменатель для дробей \(\frac{2}{9}\) и \(\frac{2}{15}\). Общий знаменатель равен 45. Приводим дроби: \(\frac{2}{9} = \frac{10}{45}\), \(\frac{2}{15} = \frac{6}{45}\). Тогда сумма равна \(\frac{10}{45} + \frac{6}{45} = \frac{16}{45}\).
Теперь упростим выражение справа. Смешанное число \(1\frac{1}{9}\) преобразуем в неправильную дробь: \(1\frac{1}{9} = \frac{10}{9}\). Вычитаем из неё \(\frac{2}{3}\). Для вычитания приведём \(\frac{2}{3}\) к знаменателю 9: \(\frac{2}{3} = \frac{6}{9}\). Тогда разность равна \(\frac{10}{9} — \frac{6}{9} = \frac{4}{9}\).
Итоговое выражение: \(\frac{16}{45} : \frac{4}{9}\). Деление заменяем умножением на обратную дробь: \(\frac{16}{45} \cdot \frac{9}{4}\). Упрощаем: \(16\) и \(4\) делятся на 4, получаем 4 и 1; \(9\) и \(45\) делятся на 9, получаем 1 и 5. В итоге остаётся \(\frac{4 \cdot 1}{5 \cdot 1} = \frac{4}{5}\).


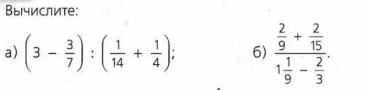


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!