ГДЗ по Математике 6 Класс Номер 177 Дорофеев, Шарыгин — Подробные Ответы

Исследуем.
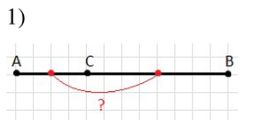
1) На отрезке АВ, длина которого равна 6 см, отмечена точка С так, что АС = 2 см. Найдите расстояние между серединами отрезков АС и СВ. Решите эту же задачу, если АB = 10 см и АС = 6 см.
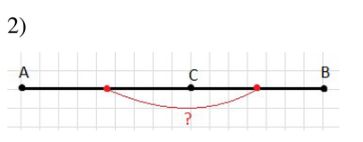
2) На отрезке АВ, длина которого равна 8 см, точка С отмечена произвольным образом. Найдите расстояние между серединами отрезков АС и СВ.
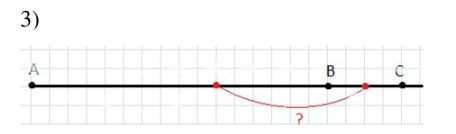
3) Изменится ли ответ, если в условии будет сказано, что точка С отмечена на прямой АВ, но не на отрезке АВ?

Исследуем задачу по точкам и отрезкам:

1) На отрезке \(AB = 6\) см точка \(C\) так, что \(AC = 2\) см. Тогда \(CB = 6 — 2 = 4\) см. Середина отрезка \(AC\) находится на расстоянии \( \frac{2}{2} = 1\) см от точки \(A\), середина отрезка \(CB\) — на расстоянии \(\frac{4}{2} = 2\) см от точки \(C\), то есть \(2 + 2 = 4\) см от точки \(A\). Расстояние между серединами: \(4 — 1 = 3\) см. Ответ: 3 см.

Если \(AB = 10\) см, \(AC = 6\) см, то \(CB = 10 — 6 = 4\) см. Середина отрезка \(AC\) отстоит от \(A\) на \(\frac{6}{2} = 3\) см, середина отрезка \(CB\) — от \(C\) на \(\frac{4}{2} = 2\) см, значит от \(A\) она на \(6 + 2 = 8\) см. Расстояние между серединами: \(8 — 3 = 5\) см. Ответ: 5 см.

2) Пусть на отрезке \(AB = 8\) см точка \(C\) делит его так, что \(AC = x\), тогда \(CB = 8 — x\). Середина \(AC\) имеет координату \(\frac{x}{2}\) от точки \(A\), середина \(CB\) — координату \(x + \frac{8 — x}{2}\). Расстояние между серединами равно \(x + \frac{8 — x}{2} — \frac{x}{2} = 4\) см. Ответ: 4 см.

3) Если точка \(C\) лежит на прямой \(AB\), но вне отрезка \(AB\), пусть \(A = 0\), \(B = 8\), \(C = 8 + t\). Тогда середина \(AC\) имеет координату \(\frac{0 + 8 + t}{2} = 4 + \frac{t}{2}\), середина \(CB\) — координату \(\frac{8 + 8 + t}{2} = 8 + \frac{t}{2}\). Их расстояние равно \(8 + \frac{t}{2} — \left(4 + \frac{t}{2}\right) = 4\) см. Ответ: не изменится, расстояние останется 4 см.

Подробный разбор задачи о взаимном расположении точек и отрезков на прямой:

1) Рассмотрим сначала отрезок \(AB\) длиной 6 см и точку \(C\) на нём так, что \(AC = 2\) см. Тогда оставшаяся часть отрезка от точки \(C\) до точки \(B\) равна \(CB = 6 — 2 = 4\) см. Чтобы найти расстояние между серединами отрезков \(AC\) и \(CB\), сначала найдём сами середины. Середина отрезка \(AC\) — это точка, которая делит его на два равных отрезка, поэтому её расстояние от точки \(A\) равно \( \frac{AC}{2} = \frac{2}{2} = 1\) см. Аналогично, середина отрезка \(CB\) делит этот отрезок пополам, значит расстояние от точки \(C\) до середины \(CB\) равно \( \frac{CB}{2} = \frac{4}{2} = 2\) см. Но точка \(C\) сама находится на расстоянии 2 см от точки \(A\), поэтому расстояние от точки \(A\) до середины отрезка \(CB\) будет \(2 + 2 = 4\) см. Теперь расстояние между серединами отрезков \(AC\) и \(CB\) — это разность их расстояний от точки \(A\): середина \(AC\) находится на 1 см от \(A\), середина \(CB\) — на 4 см от \(A\). Получаем \(4 — 1 = 3\) см. Таким образом, расстояние между серединами отрезков \(AC\) и \(CB\) равно 3 см, это и есть ответ для первого случая: 3 см.

Во втором случае первой задачи длина отрезка \(AB\) увеличена до 10 см, при этом точка \(C\) расположена так, что \(AC = 6\) см. Тогда отрезок от точки \(C\) до точки \(B\) равен \(CB = 10 — 6 = 4\) см. Опять находим середины отрезков \(AC\) и \(CB\). Середина отрезка \(AC\) делит его пополам, значит расстояние от точки \(A\) до этой середины равно \( \frac{AC}{2} = \frac{6}{2} = 3\) см. Середина отрезка \(CB\) также делит его пополам, поэтому расстояние от точки \(C\) до середины \(CB\) равно \( \frac{CB}{2} = \frac{4}{2} = 2\) см. Поскольку точка \(C\) находится на расстоянии 6 см от точки \(A\), то расстояние от точки \(A\) до середины отрезка \(CB\) будет \(6 + 2 = 8\) см. Теперь находим расстояние между серединами: оно равно разности расстояний от точки \(A\): середина \(AC\) находится на 3 см от \(A\), середина \(CB\) — на 8 см от \(A\), поэтому расстояние между ними \(8 — 3 = 5\) см. Таким образом, во втором случае первой задачи искомое расстояние между серединами отрезков \(AC\) и \(CB\) равно 5 см, что и записывается как окончательный ответ: 5 см.

2) Во второй задаче длина отрезка \(AB\) равна 8 см, а точка \(C\) выбирается на этом отрезке произвольным образом. Это означает, что \(AC\) и \(CB\) могут быть любыми положительными отрезками, суммой дающими 8 см, но нужно показать, что расстояние между серединами \(AC\) и \(CB\) всё равно получится одним и тем же числом. Обозначим длину отрезка \(AC\) через \(x\), тогда длина отрезка \(CB\) будет \(8 — x\). Середина отрезка \(AC\) лежит на расстоянии \(\frac{x}{2}\) от точки \(A\), так как делит отрезок \(AC\) пополам. Для середины отрезка \(CB\) рассуждаем так: сначала от точки \(A\) до точки \(C\) расстояние равно \(x\), а от точки \(C\) до середины \(CB\) расстояние равно половине отрезка \(CB\), то есть \(\frac{8 — x}{2}\). Поэтому координата (расстояние от точки \(A\)) середины отрезка \(CB\) равна \(x + \frac{8 — x}{2}\).

Теперь вычислим расстояние между серединами отрезков \(AC\) и \(CB\) как разность их расстояний от точки \(A\). Середина \(AC\) находится на расстоянии \(\frac{x}{2}\) от \(A\), середина \(CB\) — на расстоянии \(x + \frac{8 — x}{2}\). Значит, искомое расстояние равно \(x + \frac{8 — x}{2} — \frac{x}{2}\). Преобразуем это выражение: сначала сгруппируем члены с \(x\): \(x — \frac{x}{2} = \frac{x}{2}\), затем добавим вторую часть \(\frac{8 — x}{2}\). Получаем \(\frac{x}{2} + \frac{8 — x}{2} = \frac{x + 8 — x}{2} = \frac{8}{2} = 4\). Таким образом, независимо от того, где именно расположена точка \(C\) на отрезке \(AB\), расстояние между серединами отрезков \(AC\) и \(CB\) всегда равно 4 см. Это показывает, что ответ постоянен и не зависит от выбора точки \(C\). Окончательный ответ для второй задачи: 4 см.

3) В третьей части требуется понять, изменится ли найденное расстояние, если точка \(C\) расположена не на самом отрезке \(AB\), а на прямой, проходящей через точки \(A\) и \(B\), то есть лежит на продолжении этого отрезка. Например, пусть \(AB = 8\) см, как во второй задаче, точки \(A\) и \(B\) остаются на своих местах, но точка \(C\) лежит правее точки \(B\) на этой же прямой. Тогда можно считать, что точка \(A\) имеет координату 0, точка \(B\) — координату 8, а точка \(C\) — координату \(8 + t\), где \(t\) — некоторая положительная величина (расстояние от \(B\) до \(C\)). Теперь найдём середины отрезков \(AC\) и \(CB\) с учётом того, что это уже не две части одного отрезка, а два отрезка, один из которых длиннее, чем \(AB\).

Координата середины отрезка \(AC\) рассчитывается как среднее значение координат его концов: координаты \(A\) и \(C\) равны 0 и \(8 + t\), поэтому координата середины \(AC\) равна \(\frac{0 + 8 + t}{2} = 4 + \frac{t}{2}\). Аналогично, координата середины отрезка \(CB\) равна среднему значению координат точек \(C\) и \(B\), то есть \(\frac{8 + t + 8}{2} = \frac{16 + t}{2} = 8 + \frac{t}{2}\). Теперь найдём расстояние между этими серединами: оно равно разности координат второй и первой середины, то есть \(8 + \frac{t}{2} — \left(4 + \frac{t}{2}\right)\). При вычитании \(\frac{t}{2}\) сокращается, остаётся \(8 — 4 = 4\) см. Видно, что результат не зависит от значения \(t\), то есть от того, насколько далеко от точки \(B\) отодвинута точка \(C\). Это означает, что даже если точка \(C\) лежит не на отрезке \(AB\), а на его прямом продолжении, расстояние между серединами отрезков \(AC\) и \(CB\) остаётся таким же, как во второй задаче, то есть 4 см. Следовательно, ответ не изменится: расстояние между серединами будет равно 4 см.