ГДЗ по Математике 6 Класс Номер 176 Дорофеев, Шарыгин — Подробные Ответы

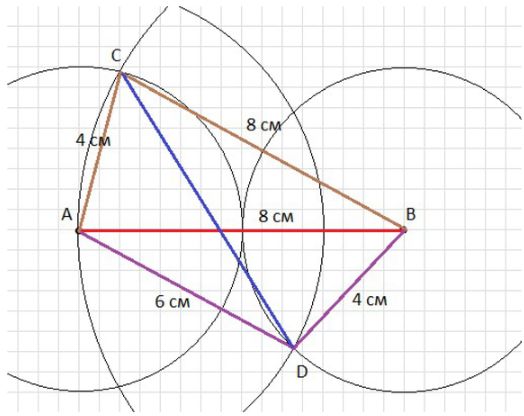
Постройте четыре точки А, В, С и D по следующему условию: точки С и D лежат по разные стороны от прямой, проходящей через точки А и B, АB = 8 см, АС = 4 см, СВ = 8 см, AD = б см, DB = 4 см. Чему равно расстояние между точками С и D?

Задача: Построить четыре точки A, B, C и D по условиям:

• Точки C и D лежат по разные стороны от прямой, проходящей через A и B.
• Отрезок AB = 8 см.
• Отрезок AC = 4 см.
• Отрезок CB = 8 см.
• Отрезок AD = 6 см.
• Отрезок DB = 4 см.

Нужно найти расстояние между точками C и D.

Решение:

1. Анализ условий:

• Точки A и B лежат на одной прямой, расстояние между ними 8 см.
• Точка C расположена так, что AC = 4 см, CB = 8 см.
• Точка D расположена так, что AD = 6 см, DB = 4 см.
• Точки C и D находятся по разные стороны от прямой AB.

2. Построение координатной системы:

• Положим точку A в начало координат (0,0).
• Точку B расположим на оси X в точке (8,0), так как AB = 8 см.
• Точку C расположим так, что расстояние AC = 4 см и CB = 8 см. Расстояние CB = 8 см больше длины AB, значит C лежит не на отрезке AB, а вне прямой AB, по одну сторону.
• Точка D расположена по другую сторону от прямой AB.

3. Нахождение координат точек C и D:

Обозначим координаты точек:

• A = (0, 0)
• B = (8, 0)
• C = (x_C, y_C)
• D = (x_D, y_D)

Используем данные расстояния:

• AC = 4 см ⇒ √(x_C² + y_C²) = 4 ⇒ x_C² + y_C² = 16.
• CB = 8 см ⇒ √((x_C − 8)² + y_C²) = 8 ⇒ (x_C − 8)² + y_C² = 64.
• AD = 6 см ⇒ √(x_D² + y_D²) = 6 ⇒ x_D² + y_D² = 36.
• DB = 4 см ⇒ √((x_D − 8)² + y_D²) = 4 ⇒ (x_D − 8)² + y_D² = 16.

4. Решаем систему для точки C:

Вычислим разность уравнений для C:
(1) x_C² + y_C² = 16
(2) (x_C − 8)² + y_C² = 64
Вычтем (1) из (2):
(x_C − 8)² − x_C² = 64 − 16 = 48
Раскроем квадрат:
x_C² − 16x_C + 64 − x_C² = 48
−16x_C + 64 = 48
−16x_C = −16
x_C = 1.

Подставим x_C = 1 в (1):
1² + y_C² = 16 ⇒ y_C² = 15 ⇒ y_C = ±√15 ≈ ±3.87.

5. Аналогично решим для точки D:

(3) x_D² + y_D² = 36
(4) (x_D − 8)² + y_D² = 16
Вычтем (3) из (4):
(x_D − 8)² − x_D² = 16 − 36 = −20
Раскроем квадрат:
x_D² − 16x_D + 64 − x_D² = −20
−16x_D + 64 = −20
−16x_D = −84
x_D = 5.25.

Подставим x_D = 5.25 в (3):
(5.25)² + y_D² = 36 ⇒ 27.56 + y_D² = 36 ⇒ y_D² = 8.44 ⇒ y_D = ±2.90.

6. Определяем расположение точек C и D по разные стороны от прямой AB (оси X):

Пусть точка C имеет координаты (1, +3.87), а точка D — (5.25, −2.90), тогда они лежат по разные стороны от прямой AB (оси X).

7. Находим расстояние между точками C и D:

Расстояние CD = √((x_C − x_D)² + (y_C − y_D)²)
= √((1 − 5.25)² + (3.87 − (−2.90))²)
= √((−4.25)² + (6.77)²)
= √(18.06 + 45.82)
= √63.88 ≈ 7.99 см.

Ответ: Расстояние между точками C и D примерно равно 8 см.

Итог:

• Построены точки C и D по условиям задачи.
• Точки расположены по разные стороны от прямой AB.
• Расстояние между ними вычислено и составляет примерно 8 см.

Если хотите, могу помочь с чертежом или другими геометрическими задачами.

Подробное решение задачи о построении точек и вычислении расстояния между ними:

Исходные данные и постановка задачи:

• Даны точки A и B, лежащие на одной прямой, расстояние между которыми равно AB = 8 см.
• Точки C и D расположены по разные стороны от прямой, проходящей через A и B.
• Длины отрезков следующие: AC = 4 см, CB = 8 см, AD = 6 см, DB = 4 см.
• Требуется найти расстояние между точками C и D.

1. Анализ условий:

Поскольку точки A и B лежат на прямой и расстояние между ними известно, удобнее всего представить эту прямую как ось X координатной плоскости с точкой A в начале координат и точкой B в точке (8, 0).

2. Координаты точек A и B:

• A — (0, 0)
• B — (8, 0)

3. Нахождение координат точек C и D:

Точки C и D не лежат на прямой AB, а находятся по разные стороны от неё, значит, их координаты будут иметь разные знаки по оси Y.
Обозначим координаты:
C — (x_C, y_C), D — (x_D, y_D).

4. Используем расстояния AC, CB, AD, DB для составления уравнений:

• Расстояние AC = 4 см:
  √((x_C − 0)² + (y_C − 0)²) = 4 ⇒ x_C² + y_C² = 16.
• Расстояние CB = 8 см:
  √((x_C − 8)² + (y_C − 0)²) = 8 ⇒ (x_C − 8)² + y_C² = 64.
• Расстояние AD = 6 см:
  √((x_D − 0)² + (y_D − 0)²) = 6 ⇒ x_D² + y_D² = 36.
• Расстояние DB = 4 см:
  √((x_D − 8)² + (y_D − 0)²) = 4 ⇒ (x_D − 8)² + y_D² = 16.

5. Решение системы для точки C:

Вычислим разность уравнений для C:
(x_C − 8)² + y_C² − (x_C² + y_C²) = 64 − 16 = 48
Раскрывая скобки:
x_C² − 16x_C + 64 + y_C² − x_C² − y_C² = 48
−16x_C + 64 = 48 ⇒ −16x_C = −16 ⇒ x_C = 1.

Подставим x_C = 1 в уравнение x_C² + y_C² = 16:
1 + y_C² = 16 ⇒ y_C² = 15 ⇒ y_C = ±√15 ≈ ±3.87.

6. Решение системы для точки D:

Аналогично:
(x_D − 8)² + y_D² − (x_D² + y_D²) = 16 − 36 = −20
Раскрываем скобки:
x_D² − 16x_D + 64 + y_D² − x_D² − y_D² = −20
−16x_D + 64 = −20 ⇒ −16x_D = −84 ⇒ x_D = 5.25.

Подставим x_D в уравнение x_D² + y_D² = 36:
(5.25)² + y_D² = 36 ⇒ 27.56 + y_D² = 36 ⇒ y_D² = 8.44 ⇒ y_D = ±2.90.

7. Выберем расположение точек по разные стороны от прямой AB:

Пусть точка C имеет координаты (1, +3.87), а точка D — (5.25, −2.90), что соответствует условию, что они находятся по разные стороны от прямой AB (оси X).

8. Вычисление расстояния между точками C и D:

Расстояние CD вычисляется по формуле расстояния между двумя точками на плоскости:
CD = √((x_C − x_D)² + (y_C − y_D)²)
= √((1 − 5.25)² + (3.87 − (−2.90))²)
= √((−4.25)² + (6.77)²)
= √(18.06 + 45.82) = √63.88 ≈ 7.99 см.

9. Итоговый ответ:

Расстояние между точками C и D примерно равно 8 см.

10. Дополнительные замечания:

• Этот метод позволяет найти расстояние между точками, расположенными по разные стороны от прямой, используя координатный подход.
• Подобные задачи развивают пространственное мышление и навыки работы с геометрическими объектами на плоскости.
• Для практического построения можно использовать миллиметровую бумагу и транспортир.

Если нужно, могу помочь с чертежом, иллюстрациями или дополнительными примерами по данной теме.