Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 174 Дорофеев, Шарыгин — Подробные Ответы
Анализируем.
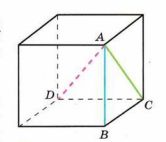
Какой из отрезков самый длинный: ребро куба АВ, диагональ грани АС или диагональ куба AD (рис. 2.27)? Какой из этих отрезков самый короткий?
Анализ длины отрезков на рисунке 2.27:
Дано:
- Куб с вершинами, обозначенными буквами A, B, C, D.
- Отрезки: ребро куба AB, диагональ грани AC, диагональ куба AD.
Цель: Определить, какой отрезок самый длинный, а какой самый короткий.
1. Длина ребра куба AB:
Пусть длина ребра куба равна a (например, AB = a).
2. Длина диагонали грани AC:
Грань куба — квадрат со сторонами длины a.
Диагональ квадрата вычисляется по формуле Пифагора:
AC = √(a² + a²) = √(2a²) = a√2.
3. Длина диагонали куба AD:
Диагональ куба — это отрезок, соединяющий противоположные вершины.
Её длина вычисляется так:
AD = √(a² + a² + a²) = √(3a²) = a√3.
4. Сравнение длин:
- AB = a.
- AC = a√2 ≈ 1,414a.
- AD = a√3 ≈ 1,732a.
Таким образом, в порядке увеличения длины:
AB < AC < AD.
5. Итог:
- Самый короткий отрезок — ребро куба AB.
- Средней длины — диагональ грани AC.
- Самый длинный — диагональ куба AD.
Заключение:
Этот результат логичен, так как диагонали всегда длиннее сторон фигуры, а диагональ куба — это самый длинный отрезок, который можно провести между его вершинами.
Если нужно, могу подробно расписать, как вычисляются длины диагоналей с примерами числовых значений.
Подробный анализ и сравнение длин отрезков на рисунке 2.27:
Исходные данные:
- Дан куб с вершинами A, B, C, D, у которого все рёбра равны по длине.
- Рассматриваются три отрезка:
- Ребро куба AB — одна из граней куба.
- Диагональ грани AC — диагональ квадратной грани куба.
- Диагональ куба AD — диагональ всего куба, соединяющая противоположные вершины.
1. Длина ребра куба AB:
Пусть длина ребра куба равна a. Это базовая единица измерения для всех других отрезков на кубе.
2. Длина диагонали грани AC:
Грань куба — квадрат со сторонами длиной a.
Чтобы найти длину диагонали квадрата, используем теорему Пифагора:
Диагональ = √(a² + a²) = √(2a²) = a√2.
Таким образом, диагональ грани длиннее ребра в √2 ≈ 1,414 раза.
3. Длина диагонали куба AD:
Диагональ куба — это отрезок, соединяющий противоположные вершины и проходящий через внутреннее пространство куба.
Её длина находится по формуле трёхмерного Пифагора:
Диагональ = √(a² + a² + a²) = √(3a²) = a√3.
Это самая длинная линия, которую можно провести между двумя точками на поверхности куба.
Значение √3 ≈ 1,732, значит диагональ куба длиннее ребра примерно в 1,732 раза.
4. Сравнение длин всех трёх отрезков:
- Ребро куба: AB = a
- Диагональ грани: AC = a√2 ≈ 1,414a
- Диагональ куба: AD = a√3 ≈ 1,732a
Порядок длин отрезков по возрастанию:
AB < AC < AD
5. Практическое значение:
- Знание этих отношений важно при решении геометрических задач, связанных с вычислением расстояний в пространстве.
- Диагональ куба часто используется в архитектуре, инженерии и дизайне для расчётов и построений.
- Также полезно понимать, как длина диагонали зависит от длины ребра, чтобы быстро ориентироваться в масштабах.
6. Пример с числовыми значениями:
Если длина ребра куба AB = 5 см, тогда:
- Диагональ грани AC = 5 × √2 ≈ 7,07 см
- Диагональ куба AD = 5 × √3 ≈ 8,66 см
7. Заключение:
Таким образом, среди указанных отрезков самый короткий — ребро куба AB, а самый длинный — диагональ куба AD. Диагональ грани AC находится по длине между ними.
Если хотите, могу подготовить иллюстрации с расчётами или помочь с похожими задачами по трёхмерной геометрии.
