Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 172 Дорофеев, Шарыгин — Подробные Ответы
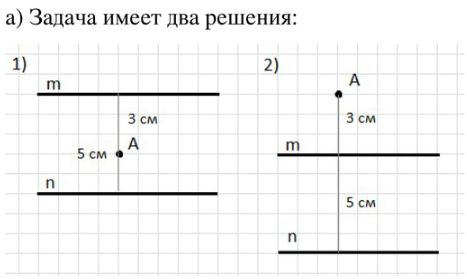
а) Расстояние между параллельными прямыми m и m равно 5 см. Точка A находится на расстоянии 3 см от прямой m. Определите расстояние от точки A до прямой n. Сколько решений имеет задача?
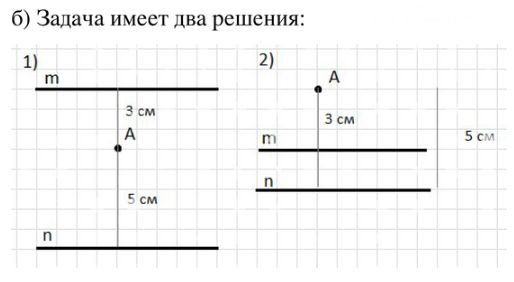
б) Точка расположена на расстоянии 3 см от одной из двух параллельных прямых и на расстоянии 5 см от другой прямой. Чему равно расстояние между параллельными прямыми?
Рассмотрим задачи подробно:
а) Расстояние между параллельными прямыми m и n равно 5 см. Точка A находится на расстоянии 3 см от прямой m. Определите расстояние от точки A до прямой n. Сколько решений имеет задача?
Анализ:
- Прямые m и n параллельны и расстояние между ними 5 см.
- Точка A находится на расстоянии 3 см от прямой m.
- Возможны два варианта расположения точки A относительно прямой n:
- Точка A лежит между прямыми m и n. Тогда расстояние от A до n будет равно разнице расстояний:
5 см − 3 см = 2 см. - Точка A находится по одну сторону от прямой m, противоположную прямой n. Тогда расстояние от A до n равно сумме:
5 см + 3 см = 8 см.
- Точка A лежит между прямыми m и n. Тогда расстояние от A до n будет равно разнице расстояний:
Ответ: Расстояние от точки A до прямой n может быть либо 2 см, либо 8 см. Задача имеет 2 решения.
б) Точка расположена на расстоянии 3 см от одной из двух параллельных прямых и на расстоянии 5 см от другой прямой. Чему равно расстояние между параллельными прямыми?
Анализ:
- Обозначим параллельные прямые как m и n.
- Точка находится так, что расстояние до одной прямой равно 3 см, до другой — 5 см.
- Рассмотрим два возможных положения точки относительно прямых:
- Если точка лежит между прямыми m и n, то расстояние между прямыми равно сумме расстояний от точки до каждой из них:
3 см + 5 см = 8 см. - Если точка находится по одну сторону от обеих прямых, то расстояние между прямыми — это разница расстояний:
|5 см − 3 см| = 2 см.
- Если точка лежит между прямыми m и n, то расстояние между прямыми равно сумме расстояний от точки до каждой из них:
Ответ: Расстояние между параллельными прямыми может быть либо 8 см, либо 2 см, в зависимости от расположения точки.
Дополнительное объяснение:
- Чтобы точно определить расстояние между прямыми, необходимо знать, с какой стороны от прямых расположена точка.
- Если точка находится между прямыми — расстояния складываются.
- Если с одной стороны — вычитаются.
Если необходимо, могу помочь с иллюстрацией или дополнительными примерами задач по этой теме.
Подробное решение и разбор задач:
а) Расстояние между параллельными прямыми m и n равно 5 см. Точка A находится на расстоянии 3 см от прямой m. Определите расстояние от точки A до прямой n. Сколько решений имеет задача?
Разбор задачи:
Даны две параллельные прямые m и n, расстояние между которыми составляет 5 см. На плоскости расположена точка A, которая находится на расстоянии 3 см от прямой m.
Нужно найти расстояние от точки A до прямой n. Рассмотрим возможные ситуации расположения точки A относительно прямых m и n.
Возможные варианты расположения точки A:
- Точка A находится между прямыми m и n. В этом случае расстояние от точки A до прямой n будет равно разности расстояния между прямыми и расстояния от точки A до прямой m.
Расчёт: 5 см − 3 см = 2 см. - Точка A находится по одну сторону от прямой m, а прямая n расположена с противоположной стороны. Тогда расстояние от точки A до прямой n будет равно сумме расстояния от точки A до прямой m и расстояния между прямыми.
Расчёт: 5 см + 3 см = 8 см.
Следовательно, в зависимости от положения точки A задача имеет два решения: расстояние от точки A до прямой n может быть как 2 см, так и 8 см.
Ответ: Расстояние от точки A до прямой n равно либо 2 см, либо 8 см. Задача имеет 2 решения.
б) Точка расположена на расстоянии 3 см от одной из двух параллельных прямых и на расстоянии 5 см от другой прямой. Чему равно расстояние между параллельными прямыми?
Разбор задачи:
Даны две параллельные прямые m и n, и точка, расположенная так, что расстояния от неё до этих прямых равны 3 см и 5 см соответственно.
Определим возможное расположение точки и вычислим расстояние между прямыми:
- Если точка расположена между прямыми m и n. Тогда расстояние между прямыми будет равно сумме расстояний от точки до каждой из них:
Расчёт: 3 см + 5 см = 8 см. - Если точка расположена с одной стороны от обеих прямых. В этом случае расстояние между прямыми равно разнице расстояний от точки до каждой из прямых:
Расчёт: |5 см − 3 см| = 2 см.
Таким образом, без дополнительной информации о расположении точки, возможны два варианта расстояния между параллельными прямыми.
Ответ: Расстояние между параллельными прямыми может быть либо 8 см, либо 2 см, в зависимости от положения точки.
Дополнительные замечания и рекомендации:
- Для точного определения расстояния между параллельными прямыми необходимо знать, где именно расположена точка — между ними или с одной из сторон.
- Если вы выполняете подобные задачи на практике, старайтесь предварительно зарисовывать схему и отмечать возможные положения точек.
- Понимание этих вариантов поможет решать задачи на построение и измерение расстояний в геометрии.
- Также эти знания пригодятся при анализе реальных ситуаций в архитектуре, строительстве и инженерии.
Заключение:
В геометрии часто встречаются ситуации, когда одно и то же условие может давать несколько решений, зависящих от расположения объектов на плоскости. Важно внимательно анализировать условие и использовать геометрические построения для точности.
Если нужно, могу помочь с иллюстрациями, схемами или дополнительными примерами по теме расстояний и параллельных прямых.
