ГДЗ по Математике 6 Класс Номер 167 Дорофеев, Шарыгин — Подробные Ответы

Действуем по алгоритму.
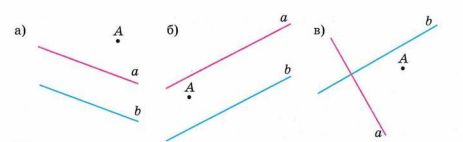
Найдите расстояние от точки A до прямой a и до прямой b (рис. 2.25, a-в).

а) Расстояние от точки \( A \) до прямой \( a \) равно 1,2 см, до прямой \( b \) — 2,5 см.

б) Расстояние от точки \( A \) до прямой \( a \) равно 0,6 см, до прямой \( b \) — 1 см.

в) Расстояние от точки \( A \) до прямой \( a \) равно 1,9 см, до прямой \( b \) — 0,7 см.

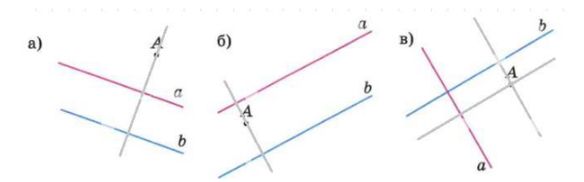
а) Для нахождения расстояния от точки \( A \) до прямой \( a \) необходимо провести перпендикуляр из точки \( A \) к прямой \( a \) и измерить длину этого перпендикуляра. На рисунке видно, что длина этого перпендикуляра равна 1,2 см, значит расстояние от точки \( A \) до прямой \( a \) равно 1,2 см. Аналогично, расстояние от точки \( A \) до прямой \( b \) измеряется как длина перпендикуляра, проведённого из точки \( A \) к прямой \( b \). Это расстояние равно 2,5 см.

б) В этом случае также необходимо провести перпендикуляры из точки \( A \) к прямым \( a \) и \( b \). Длина перпендикуляра от точки \( A \) до прямой \( a \) равна 0,6 см, а от точки \( A \) до прямой \( b \) — 1 см. Эти значения определяют минимальное расстояние от точки до прямой, так как расстояние между точкой и прямой — это именно длина перпендикуляра.

в) Для третьего рисунка расстояния измеряются по тому же принципу: расстояние от точки \( A \) до прямой \( a \) — это длина перпендикуляра, равная 1,9 см, а расстояние от точки \( A \) до прямой \( b \) — длина перпендикуляра, равная 0,7 см. Такие измерения позволяют точно определить минимальное расстояние от точки до каждой из прямых.

Таким образом, измеряя длины перпендикуляров из точки \( A \) к каждой из прямых, мы получаем искомые расстояния, которые являются кратчайшими расстояниями между точкой и прямой. Эти значения соответствуют измерениям на рисунках и равны: для а) 1,2 см и 2,5 см; для б) 0,6 см и 1 см; для в) 1,9 см и 0,7 см соответственно.