ГДЗ по Математике 6 Класс Номер 161 Дорофеев, Шарыгин — Подробные Ответы

1) Изобразите все случаи взаимного расположения трёх прямых на плоскости (случаев всего 4). Какое наибольшее число точек пересечения могут иметь три прямые?

2) На плоскости проведены четыре прямые и отмечены точки, в которых эти прямые попарно пересекаются. Какое наибольшее число таких точек могло получиться?

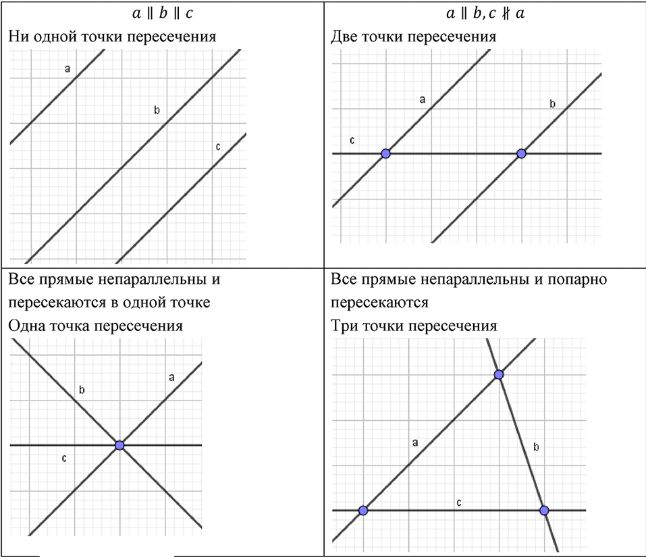
1) У трёх прямых возможны 4 случая взаимного расположения на плоскости:
1) все три параллельны — точек пересечения нет;
2) две параллельны, третья пересекает обе — две точки;
3) все три проходят через одну точку — одна точка;
4) каждая пара пересекается в своей точке (нет параллельных и нет общей точки для трёх прямых) — три точки.
Следовательно, наибольшее число точек пересечения трёх прямых равно 3.

2) Четыре прямые пересекаются попарно. Число пар прямых равно числу сочетаний из 4 по 2: \(C_4^2=\frac{4\cdot3}{2}=6\). Если ни одна пара не параллельна и никакие три прямые не проходят через одну точку, все 6 точек будут различными.
Следовательно, наибольшее число точек попарного пересечения четырёх прямых равно 6.

1) Рассмотрим все возможные случаи взаимного расположения трёх прямых на плоскости. Первый случай: все три прямые параллельны, тогда они никогда не пересекаются, множество точек пересечения равно \(\emptyset\). Второй случай: две прямые параллельны, а третья наклонена так, что пересекает каждую из них, в результате получаются ровно две различные точки пересечения. Третий случай: все три прямые проходят через одну и ту же точку, тогда все попарные пересечения совпадают в одной точке, поэтому получается одна общая точка пересечения. Четвёртый, самый важный случай: ни одна пара прямых не параллельна и никакие три прямые не пересекаются в одной и той же точке; тогда каждая пара прямых даёт свою, отдельную точку пересечения.

В этом четвёртом случае можно перечислить пары прямых: первая и вторая пересекаются в одной точке, первая и третья пересекаются во второй точке, вторая и третья пересекаются в третьей точке. Таким образом, у нас всего три пары прямых, и каждая из них даёт одну уникальную точку пересечения, то есть получаем три различные точки. Важно понимать, что больше трёх различных точек пересечения быть не может, потому что всего имеется три прямые, а каждая точка пересечения всегда возникает как результат пересечения некоторой пары прямых. Поскольку пар прямых здесь ровно три, то максимум три точки пересечения. Поэтому во всех возможных конфигурациях трёх прямых на плоскости наибольшее число точек пересечения достигается именно в этом четвёртом случае и равно 3.

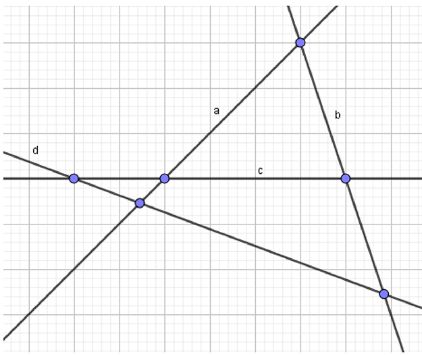
2) Теперь рассмотрим четыре прямые на плоскости. Нас интересуют точки, в которых прямые попарно пересекаются, то есть каждые две прямые образуют одну точку пересечения, если они не параллельны. Число различных пар прямых из четырёх можно посчитать с помощью сочетаний: нужно выбрать 2 прямые из 4, это даёт \(C_4^2=\frac{4\cdot3}{2}=6\) пар. Если удастся расположить прямые так, чтобы ни одна пара не была параллельной, то каждая из этих шести пар даст по одной точке пересечения. Однако, чтобы эти точки были действительно разными, нужно дополнительно потребовать, чтобы никакие три прямые не пересекались в одной точке, иначе одна точка пересечения принадлежала бы сразу трём парам, и количество различных точек уменьшилось бы.

Поэтому располагаем прямые так, чтобы каждая пара пересекалась и чтобы в одной точке пересекались только две прямые. В этом случае первая и вторая прямые дают одну точку, первая и третья дают вторую, первая и четвёртая – третью, вторая и третья – четвёртую, вторая и четвёртая – пятую, третья и четвёртая – шестую точку. Все эти точки можно сделать различными именно за счёт того, что прямые не параллельны и никаких тройных пересечений нет. Так как число пар не может быть больше шести, то и больше шести различных точек пересечения получить невозможно. Следовательно, наибольшее число точек попарного пересечения четырёх прямых на плоскости равно 6.