
Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Математике 6 Класс Номер 159 Дорофеев, Шарыгин — Подробные Ответы
Действуем по алгоритму.
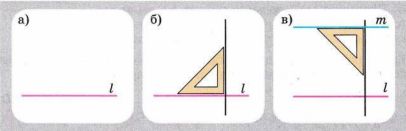
На рисунке 2.20, a-в показан способ построения прямой, параллельной данной, с помощью одного угольника. На каком свойстве параллельных прямых основан этот способ? Начертите какую-нибудь прямую и постройте с помощью угольника прямую, ей параллельную.
Действуем по алгоритму на рисунке 2.20 (a-в): построение прямой, параллельной данной с помощью одного угольника.
На каком свойстве параллельных прямых основан этот способ?
Этот способ построения основан на свойстве, что прямые, пересекаясь с третьей прямой (секущей), образуют равные соответственные углы.
Если одна из прямых проведена, а другая построена так, что соответственные углы при секущей равны, то эти две прямые параллельны.
Описание способа (по рисункам):
- Рисунок a: проведена исходная прямая l.
- Рисунок б: угольник поставлен так, чтобы одна из его сторон совпадала с прямой l, а другая — была ориентирована под нужным углом.
- Рисунок в: угольник сдвинут параллельно линии l и установлен так, чтобы нижняя сторона угольника была параллельна исходной прямой l, а другая сторона — указывала направление новой прямой m.
- Проведена новая прямая m по стороне угольника — она будет параллельна l.
Пошаговая инструкция для самостоятельного построения:
- Начертите на листе произвольную прямую и обозначьте её l.
- Приложите угольник к прямой l так, чтобы одна сторона угольника совпала с прямой l.
- Обозначьте направление второй стороны угольника (перпендикулярной к первой) — по ней будет построена новая прямая.
- Не меняя угла наклона угольника, сдвиньте его так, чтобы нижняя сторона угольника проходила через новую точку (например, точку А), где хотите провести параллельную прямую.
- Проведите прямую по стороне угольника — это будет прямая m, параллельная l.
Итог:
- Данный способ позволяет построить параллельную прямую с помощью одного угольника, используя свойство равенства соответственных углов при пересечении секущей.
- Этот метод удобен и точен, если аккуратно придерживаться положения угольника и параллельного сдвига.


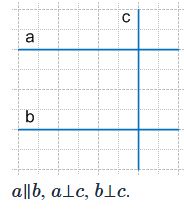


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!