ГДЗ по Математике 6 Класс Номер 158 Дорофеев, Шарыгин — Подробные Ответы

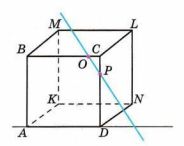
На рёбрах куба взяты точки O и P (рис. 2.19). Пересекает ли прямая ОР прямые AD, ML, АВ, DN, ВМ?
Указание. Воспользуйтесь моделью куба; в качестве прямых можно использовать, например, карандаши, вязальные спицы и т.д.

Прямая \( OP \) пересекает прямые \( AD \) и \( AB \), так как они лежат в одной плоскости.

Прямая \( OP \) не пересекает прямые \( ML \), \( DN \) и \( BM \), так как они лежат в разных плоскостях и являются скрещивающимися прямыми.

Прямая \( OP \) пересекает прямые \( AD \) и \( AB \), потому что все эти прямые лежат в одной плоскости. В данном случае это плоскость грани куба, на которой находятся точки \( A \), \( B \), \( D \), а также точки \( O \) и \( P \). Поскольку прямые \( AD \) и \( AB \) принадлежат этой плоскости, и прямая \( OP \) также лежит в ней, то они могут пересекаться. Пересечение происходит в точках, где линии фактически пересекаются на рисунке, что подтверждается визуальной моделью куба.

Прямые \( ML \), \( DN \) и \( BM \) лежат в других плоскостях куба, отличных от той, где находится прямая \( OP \). Эти прямые расположены на различных гранях куба, которые не совпадают с плоскостью, содержащей \( OP \). Из-за этого они не могут пересекаться с прямой \( OP \), так как находятся в пространстве по-разному. Такие прямые называются скрещивающимися — они не параллельны и не пересекаются, потому что лежат в разных плоскостях.

Таким образом, для проверки пересечения прямой \( OP \) с другими прямыми важно учитывать, лежат ли они в одной плоскости. Если да, то пересечение возможно, если нет — прямые либо параллельны, либо скрещиваются. В данном случае прямая \( OP \) пересекает только те прямые, которые находятся в той же плоскости, то есть \( AD \) и \( AB \), и не пересекает \( ML \), \( DN \) и \( BM \), так как они лежат в разных плоскостях.