Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 157 Дорофеев, Шарыгин — Подробные Ответы
Верно или неверно.
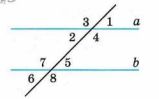
Прямые a и b параллельны, угол 1 = 45 градусов (рис. 2.18). Верно ли, что:
1) угол 2 = угол 1 = 45 градусов;
2) угол 5 = угол 1 = 45 градусов;
3) угол 4 = 180 градусов — угол 1 = 135 градусов?
Назовите величины углов, обозначенных цифрами б, 7 и 8.
Рассмотрим рисунок 2.18 и ответим на вопросы.
Дано:
- Прямые a и b параллельны.
- Угол 1 равен 45°.
1) Верно ли, что угол 2 = угол 1 = 45°?
Углы 1 и 2 — это вертикальные углы, образованные пересечением прямых и секущей.
Вертикальные углы равны.
Следовательно, угол 2 = 45°.
Утверждение верно.
2) Верно ли, что угол 5 = угол 1 = 45°?
Угол 5 — соответственный угол к углу 1, так как прямые a и b параллельны и пересечены секущей.
Соответственные углы равны.
Следовательно, угол 5 = 45°.
Утверждение верно.
3) Верно ли, что угол 4 = 180° − угол 1 = 135°?
Углы 1 и 4 — смежные углы, сумма которых равна 180°.
Следовательно, угол 4 = 180° − 45° = 135°.
Утверждение верно.
4) Назовите величины углов, обозначенных цифрами 6, 7 и 8.
- Угол 6 — вертикальный к углу 5, значит, угол 6 = угол 5 = 45°.
- Угол 7 — вертикальный к углу 4, значит, угол 7 = угол 4 = 135°.
- Угол 8 — соответственный угол к углу 4, значит, угол 8 = 135°.
Подробный разбор задания по рисунку 2.18:
Исходные данные:
- Прямые a и b параллельны.
- Угол 1 равен 45°.
1) Проверка утверждения: угол 2 = угол 1 = 45°
Углы 1 и 2 — это вертикальные углы, так как они образуются при пересечении двух прямых и лежат друг напротив друга.
По свойству вертикальных углов они равны.
Значит:
угол 2 = 45°.
Утверждение верно.
2) Проверка утверждения: угол 5 = угол 1 = 45°
Угол 5 — это соответственный угол к углу 1, поскольку прямые a и b параллельны, а секущая пересекает их.
Согласно свойству соответственных углов, они равны.
Значит:
угол 5 = 45°.
Утверждение верно.
3) Проверка утверждения: угол 4 = 180° − угол 1 = 135°
Углы 1 и 4 — смежные, так как они имеют общую сторону и лежат на одной прямой.
Сумма смежных углов равна 180°:
угол 4 = 180° − угол 1 = 180° − 45° = 135°.
Утверждение верно.
4) Определение величин углов, обозначенных цифрами 6, 7 и 8:
- Угол 6: вертикальный угол к углу 5, значит угол 6 = угол 5 = 45°.
- Угол 7: вертикальный угол к углу 4, значит угол 7 = угол 4 = 135°.
- Угол 8: соответственный угол к углу 4, значит угол 8 = 135°.
Дополнительные пояснения по свойствам углов:
- Вертикальные углы — это углы, образованные при пересечении двух прямых и расположенные друг напротив друга; они равны.
- Смежные углы — это углы, имеющие общую сторону, а две другие стороны лежат на одной прямой; сумма смежных углов равна 180°.
- Соответственные углы — это углы, которые находятся по одну сторону от секущей и при этом лежат на параллельных прямых; они равны.
Итог:
- Все утверждения (1), (2) и (3) верны.
- Величины углов 6, 7 и 8 равны соответственно 45°, 135° и 135°.
- Понимание этих свойств углов важно для решения различных задач по геометрии, связанных с параллельными прямыми и пересечениями.
Если нужно, могу дополнительно объяснить, как находить углы на подобных рисунках, или дать примеры с другими фигурами.
