Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 155 Дорофеев, Шарыгин — Подробные Ответы
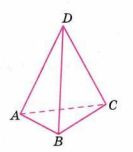
Какие рёбра пирамиды, изображённой на рисунке 2.17, принадлежат скрещивающимся прямым? Назовите все пары рёбер.
Анализ пар рёбер пирамиды, принадлежащих скрещивающимся прямым:
Скрещивающимися прямыми являются пары рёбер:
- ВС и AD
- AB и CD
Все пары рёбер:
- AC и BD
- ВС и AD
- AB и CD
Объяснение:
Пары рёбер, перечисленные выше, не пересекаются и не лежат в одной плоскости, поэтому являются скрещивающимися прямыми.
Важно понимать, что скрещивающиеся прямые — это такие прямые, которые не пересекаются и не параллельны, при этом не лежат в одной плоскости.
Если нужна дополнительная информация или пояснения, сообщите!
Подробный анализ пар рёбер пирамиды и их взаимного расположения:
Определение скрещивающихся прямых:
Скрещивающиеся прямые — это такие прямые, которые одновременно удовлетворяют следующим условиям:
- не лежат в одной плоскости;
- не пересекаются;
- не являются параллельными.
Это значит, что скрещивающиеся прямые не могут встретиться при продлении, но и не находятся в одном геометрическом уровне.
Пары рёбер пирамиды, которые являются скрещивающимися прямыми:
- ВС и AD:
Ребро ВС — это сторона основания, а ребро AD — боковое ребро пирамиды. Они не пересекаются, не параллельны и не лежат в одной плоскости, поэтому являются скрещивающимися. - AB и CD:
Аналогично, ребра AB и CD расположены так, что они не пересекаются и не лежат в одной плоскости, поэтому тоже скрещивающиеся.
Все пары рёбер, упомянутые в условии:
- AC и BD
- ВС и AD
- AB и CD
Объяснение отличий:
Пары ВС и AD и AB и CD — именно скрещивающиеся прямые, так как они не лежат в одной плоскости.
Пара AC и BD обычно лежит в основании пирамиды (или в одной плоскости) и может быть либо пересекающейся, либо параллельной, в зависимости от формы пирамиды.
Поэтому, в контексте скрещивающихся прямых выделяются именно первые две пары.
Практическое значение:
- Понимание скрещивающихся прямых важно в пространственной геометрии, так как они встречаются в многогранниках и объёмных телах.
- Это помогает решать задачи на нахождение расстояния между прямыми, углов между ними и многое другое.
Вывод:
Таким образом, ВС и AD, а также AB и CD — это пары рёбер пирамиды, которые являются скрещивающимися прямыми, поскольку не пересекаются, не параллельны и не лежат в одной плоскости.
Пара AC и BD включена в список для полного описания рёбер, но не является скрещивающейся.
Если нужна помощь с иллюстрациями или дополнительным объяснением, как определить скрещивающиеся прямые — обращайтесь!
