Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 153 Дорофеев, Шарыгин — Подробные Ответы
Начертите в тетради по линиям сетки:
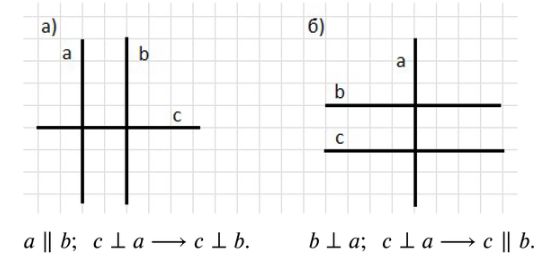
а) две параллельные прямые a и b и прямую c, перпендикулярную прямой a;
б) прямую a и прямые b и c, ей перпендикулярные.
В каждом случае охарактеризуйте взаимное расположение прямых c и b.
Задание: Начертите в тетради по линиям сетки:
а) две параллельные прямые a и b и прямую c, перпендикулярную прямой a;
Построение:
- Проведите две параллельные прямые a и b. По сетке это могут быть горизонтальные линии, расположенные на некотором расстоянии друг от друга.
- Проведите прямую c, которая пересекает прямую a под прямым углом (90°), то есть c — перпендикулярна a. По сетке это вертикальная линия, пересекающая a.
Взаимное расположение прямых c и b:
- Поскольку a и b — параллельны, а c перпендикулярна a, то c также перпендикулярна b (перпендикуляр к параллельным прямым).
- Таким образом, прямые c и b — перпендикулярны.
б) прямую a и прямые b и c, ей перпендикулярные.
Построение:
- Проведите прямую a — например, горизонтальную линию по сетке.
- Проведите две прямые b и c, которые обе перпендикулярны прямой a, то есть вертикальные линии, пересекающие a под прямым углом.
Взаимное расположение прямых c и b:
- Прямые b и c обе перпендикулярны прямой a, но расположены параллельно друг другу (обе вертикальны и не пересекаются).
- Следовательно, прямые b и c — параллельны.
Вывод:
- В первом случае (а) прямые c и b — перпендикулярны.
- Во втором случае (б) прямые c и b — параллельны.
Если нужна помощь с рисунками или дополнительными объяснениями — скажи!
