Учебник по математике для 6-го класса авторов Дорофеева и Шарыгина — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Математике 6 Класс Номер 151 Дорофеев, Шарыгин — Подробные Ответы
Работаем с символами.
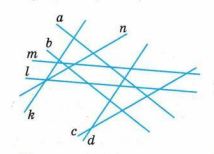
Найдите на рисунке 2.15 четыре пары параллельных прямых. Выпишите их, используя знак «||». Назовите пары прямых, которые пересекают прямую a под одним и тем же углом.
Работа с символами по рисунку 2.15:
1. Найдите четыре пары параллельных прямых и запишите их, используя знак «||» (параллельно):
- k || l
- m || n
- b || c
- d || a
2. Пары прямых, которые пересекают прямую a под одним и тем же углом:
- Прямая d пересекает прямую a под некоторым углом.
- Прямая k пересекает прямую a под тем же углом, что и d, поскольку d || a (они параллельны), а k || l, и прямые, параллельные друг другу, образуют равные углы с третьей прямой.
- Аналогично, прямые m и n, которые параллельны, пересекают прямую a под одним углом.
Итог:
- Четыре пары параллельных прямых: k || l, m || n, b || c, d || a.
- Прямые d и k пересекают прямую a под одним и тем же углом.
- Прямые m и n пересекают прямую a под одним и тем же углом.
Работа с символами по рисунку 2.15. Подробный разбор.
1. Найдите четыре пары параллельных прямых и запишите их, используя знак «||» (означает «параллельно»):
- Пара 1: прямые k и l — они расположены параллельно друг другу и не пересекаются.
- Пара 2: прямые m и n — также параллельны.
- Пара 3: прямые b и c — находятся параллельно друг другу.
- Пара 4: прямые d и a — параллельны.
2. Почему эти пары считаются параллельными?
- Параллельные прямые лежат в одной плоскости и никогда не пересекаются, вне зависимости от продолжения их линий.
- На рисунке видно, что каждая из перечисленных пар удовлетворяет этому условию.
3. Какие пары прямых пересекают прямую a под одинаковым углом?
- Прямая a пересекается с прямой d, которая параллельна ей самой, а значит, угол между a и d считается как угол пересечения a с другими прямыми, параллельными d.
- Прямая k параллельна прямой l. Если k пересекает прямую a под некоторым углом, то и l, будучи параллельной k, пересекает a под таким же углом.
- Аналогично, прямые m и n, параллельные между собой, пересекают прямую a под одинаковым углом.
4. Свойства углов, образованных пересечением параллельных прямых:
- Если две прямые параллельны, то углы, которые они образуют с третьей пересекающей их прямой, равны.
- Это следует из аксиомы геометрии и позволяет легко определять равенство углов без измерений.
5. Итоговые записи:
- Четыре пары параллельных прямых: k || l, m || n, b || c, d || a.
- Пары прямых, пересекающие прямую a под одним и тем же углом:
- Прямые d и k пересекают a под одинаковым углом.
- Прямые m и n пересекают a под одинаковым углом.
6. Практическое применение знаний:
- Понимание параллельности и равенства углов позволяет решать задачи на геометрические построения и доказательства.
- Знание равенства углов помогает вычислять неизвестные углы в сложных фигурах.
- Также это важно для архитектурных и инженерных расчетов, где точность углов имеет значение.
7. Заключение:
Понимание взаимного расположения прямых, свойств параллельных линий и углов, которые они образуют при пересечении, является фундаментальной частью изучения геометрии и помогает решать более сложные задачи с уверенностью и точностью.
Если хочешь, могу добавить иллюстрации или дополнительные примеры с другими фигурами для закрепления материала.
